Classifying Triangles
Angle Relationships
Polygons
Similar Triangles
Exterior/Interior Angles
100
This triangle has sides that measure 15,16 and 17.
What is a scalene triangle?
100
These angles have a sum of 90 degrees.
What are complementary angles?
100
This can be found by dividing the number of outside angles by 360.
What is the measurement of each exterior angle?
100
This theorem has 2 triangles with 3 proportional sides.
What is side-side-side similarity?
100
These are inside angles on the same side of the transversal that are supplementary.
What are same-side interior angles?
200
This type of triangle has three angles that each measure 60 degrees and each side measures 10 units.
What is acute equilateral?
200
These angles have the same measurement.
What are congruent angles?
200
Use (n-2)*180 to find this measurement of a polygon.
What is the sum of the interior angles?
200
This theorem states that 2 triangles have two pairs of congruent angles.
What is angle-angle similarity?
200
These are two interior angles on opposite sides of the transversal that are congruent.
What are alternate interior angles?
300
This type of triangle has 3 angles that measure 145, 15 and 20.
What is an obtuse angle?
300
These angles are side by side and may or may not be congruent.
What are adjacent angles?
300
The sum of the interior angles of a heptagon.
What is 900 degrees?
300
This theorem says that 2 triangles have two pairs of proportional sides and congruent angles between them.
What is side-angle-side similarity?
300
Name this type of angle relationship.
What are alternate exterior angles?
400
This triangle has a 90 degree angle and two sides that measure 32 units each.
What is a right isosceles?
400
These two angles are formed by intersecting sides and are always congruent.
What are vertical angles?
400
This is always 360 degrees.
What is the sum of the exterior angles?
400
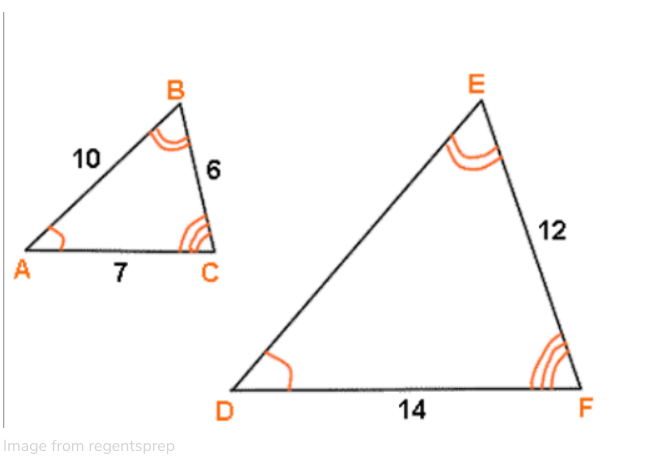These two triangles have this type of similarity.
What is angle-angle similarity?
400
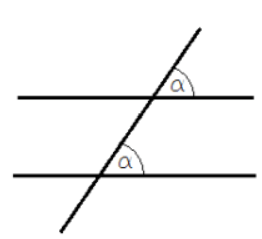Name this type of angle relationship.
What are corresponding angles?
500
This triangle has three sides that are congruent and three angles that are congruent.
What is an equiangular equilateral triangle?
500
These 2 angles have a sum of 180 degrees.
What are supplementary angles?
500
This is found by dividing the sum of the interior angles by the number of interior angles.
What is the measure of each interior angle?
500
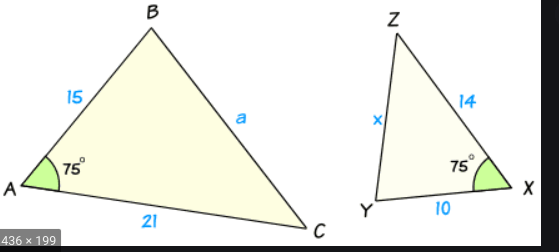These two triangles have this type of similarity.
What is side-angle-side similarity?
500
These types of angle relationships are congruent.
What are corresponding angles, alternate exterior angles and alternate interior angles?