Particles
Applications of Integrals
Intervals
Rotational Solids
Optimization
100
For t>=0, a particle moves along the x-axis. The velocity of the particle is given below and at time t = 2, x = 6. It's the total distance traveled by the particle between t = 0 and t = 3
v(t)=4t+5
What is 33?
100
Given that f(1) = 2 and f'(x) = 9x, determine f(-2).
What is -34 ?
100
On the interval [0, 7] ,0 < f'(x) < f''(x) < 3. If f(0) = 5, it's whether f(7) can be 27.
What is false (since f(7) can at most be 26).
100
It's the integral representing the volume of the solid formed by rotating the region bound by y = x^2+1, y= x + 7 and y = 7 in the first quadrant.
What is...
int_7^10((sqrt(y-1))^2-(y-7)^2)dy
100
A rectangular pen is being constructed against a wall, so that 3 of the sides require fencing. If the pen needs to be 100 ft^2 in area and the fencing costs $10 per square foot, it's the dimensions that minimize the cost.
What is...
l=5sqrt2 , w = 10sqrt2
200
A particle moves along the x-axis with velocity given below. At time t = 0, x = 14.3. Determine the position of the particle at time t = 1.
v(t)=3t^2+6t
What is 18.3 ?
200
int_3^0x(x^2+x/3)dx
What is...
-81/4-9=-117/4
200
It's the sketch of a graph that meets the criteria of the Extreme Value Theorem but does not meet the criteria of the Mean Value Theorem.
What is a function that is continuous but not differentiable?
200
Region N is formed by the graphs of y=x^2, y = 4x, x = 4 and the x-axis. It's the volume of the solid created by rotating N about the line y = -2 expressed as an integral.
What is...
piint_0^4((4x)^2-(x^2)^2)dx
200
Two sailboats leave a lighthouse at the same time. The blue sailboat moves north at 5 mph while the green sailboat moves east at 4 mph. It's the rate of change of the distance between the two sailboats after 3 hours.
What is...
123/sqrt361 mph
300
A particle is moving along the x-axis with acceleration given below for 0<=t<=10 with v(t) = -6 at t = 0. It's the intervals in which the particle is moving to the left and right for the interval [0, 10]
a(t)=2t-1
What is moving to the left on (0,3) and to the right on (3,10) ?
300
It's the volume of a solid with a base bound by y = x^3 and y= x^2 with cross sections perpendicular to the x-axis that are equilateral triangles.
What is...
sqrt3/420
300
A function f is defined on [0, 8] and has horizontal tangents at x = 2 and x = 5 as well as zeros at x = 0, x= 4 and x = 6. For the function g(x) defined below, determine all points of inflection of the graph.
g(x)=int_2^xf(x)dx
What is x = 2 and x = 5 ?
300
It's the volume of the region bound by the equations below rotated about the y-axis:
y=sqrtx, x = 4, y = 0
What is...
(128pi)/5
300
It's the point on the parabola y = x^2 that is closest to (3, 0)
What is (3/2, 9/4) ?
400
It's the position of a model train along a linear track with position 0 at t = 0 and velocity v(t) given below at time t = 1/3.
v(t)=(x+6)/(9x^3+54x^2+x+6)
What is pi/12 ?
400
It's the area enclosed by the regions formed on the interval [0, 8] by the following functions given that points of intersection occur at (0, 1), (4, 2) and (8, 1)
y=cos(pix/8)+2 , y= (-x+4)/2
What is...
16/pi-4
400
It's the maximum and minimum number of points of inflection a polynomial function of odd degree n can have.
What is a minimum of 1 and a maximum of n-2?
400
It's the volume of the solid formed by rotating the region bound by y = cos(x^2), the x-axis and x=1 about the line x = 1 pictured below:
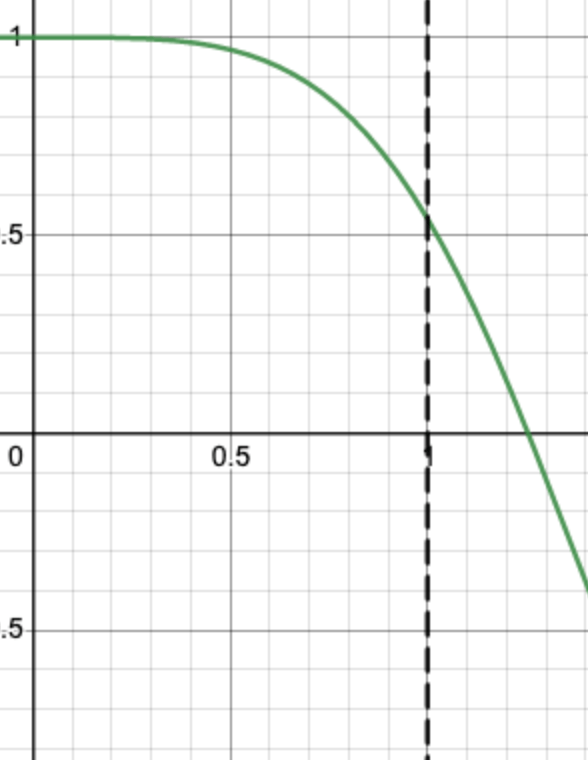
What is...
pisin(1)
400
A rectangular room is being designed with an open roof that must have a volume of 40m^3. The length of the base must be 3 times the width of the base. The cost for the base of the room is $30 per square meter while the costs of the sides is $10 per square meter. It's the equation that would determine the width that gives the minimum cost of the room.
What is...
0=270w^2-3200/(3w^2)
500
It's the total distance traveled by the particle on the interval [0, 1000] with the position function...
x(t)=sin(pi/2t)
What is...
2000/pi
500
The rate at which people enter a museum is modeled by the function given below, where t is in hours. If there are five people at the museum when t = sqrt(6)/2, it's the number of people that have entered the museum at time t = sqrt(2)
What is...
5+sqrt(6)/4
500
Let g(x) be a differentiable function with g(2) = 7 and g'(2) = -8 . It's the estimate for g(0.5) using linear approximation.
What is 19?
500
It's the volume of the solid generated by revolving the regions bound by the functions below about the line y= 1 (Calculators OK!)
y=|sinx| , y = (x-pi)^2
What is 1.146 ?
500
A rectangle is inscribed inside a circle of radius r with length l and width w. It's the dimensions of the rectangle in terms of r that maximizes the quantity lw^2
What is...
l=(2rsqrt3)/3 , w = (2rsqrt6)/3