Binomial
Geometric
Random Variables
According to Russo
Combining Random Variables
100
Name the four conditions for a Binomial Distribution.
Fixed number of trials
Independent Trials
Equal Probability of Success
Each trial can result in a success or failure
100
A geometric distribution focuses on the ____________ success.
First
100
Let X = the height of a randomly selected student from our class. What type of random variable is X?
Continuous
100
Greatest quarterback of all time.
Eli Manning
100
Let
sigmax = 3 and sigmay = 5
sigma (x+y)
Need to know they are independent
200
HMHS is a population of 800 students of which the percent of students who ate breakfast is fixed. You're choosing a sample and counting the number of students ate breakfast today. How large of a sample can you take and still treat this problem as Binomial?
80
200
A scratch off is 20% likely to be a winner of some sort. You decide to purchase tickets until you win. What is the probability that you only purchase two tickets?
.16
200
You are playing a lottery, which costs $2, in which the expected winning on each ticket is .89$. Explain what this means in regards to how much you lose when you play.
Over many tickets, the player would lose around $1.11 on each ticket.
200
Greatest High School Sport
Cross Country
200
Suppose we know Reid runs normally with a mean of 4.58 minutes in a 1600 and a standard deviation of .42 minutes.
Suppose we know Ben runs normally with a mean of 5.02 minutes in a 1600 and a standard deviation of .28 minutes. Find the average combined time if both boys ran the 1600.
9.60 minutes
300
Blaise is 68% likely to make free throws at Intermural Basketball. In a sample of 15 shots, what is the probability that he makes exactly 9? Must show work with substitutions.
15C9 (.68)^9(.32)^6
.1671
300
A scratch off is 20% likely to be a winner of some sort. How many tickets can you expect to purchase before you win?
5
300
Let X by the amount of money won on a lotter ticket.
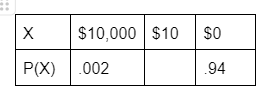
Find P(X = $10)
.058
300
Greatest baseball player of all time
Ronald Acuna
300
Suppose we know Reid runs normally with a mean of 4.58 minutes in a 1600 and a standard deviation of .42 minutes.
Suppose we know Ben runs normally with a mean of 5.02 minutes in a 1600 and a standard deviation of .28 minutes. If the two were to run independently of each other, find the standard deviation of Reid's time + Ben's time.
.505 minutes
400
Blaise is 68% likely to make free throws at Intermural Basketball. In a sample of 15 shots, what is the probability that he makes more than 9 shots? Must show work with substitutions.
15C10 (.68)^10(.32)^5+...+.68^15
.6607
400
A scratch off is 20% likely to be a winner of some sort. You purchase tickets until you win. What is the probability that you purchase less than 5 tickets? Show work and answer
.2+...+.8^3(.2)
.5904
400
Find and interpret the expected value of X, the amount won on a single lottery ticket.
Over many ticket purchases, the ticket will pay about $2.46 (minus the cost of the ticket)
400
Statisticians never get
Lucky
400
Suppose we know Reid runs normally with a mean of 4.58 minutes in a 1600 and a standard deviation of .42 minutes.
Suppose we know Ben runs normally with a mean of 5.02 minutes in a 1600 and a standard deviation of .28 minutes.
The two boys runs a 2 man relay in which each runs a 1600, independently of the other. Find the probability that their total time is slower than 10 minutes. Show all work for credit.
.2148
500
Blaise is 68% likely to make free throws at Intermural Basketball. In a sample of 15 shots, what is the probability that he makes between 6 and 9 shots inclusive? Must show work with substitutions.
15C6(.68)^6(.32)^9+...+15C9(.68)^9(.32)^6
.3331
500
A scratch off is 20% likely to be a winner of some sort. You decide to purchase tickets until you lose. What is the probability that you purchase more than 5 tickets? Show work and answer
1- (.8+...+.8(.2)^4)
.0003
500
Find, and interpret, the standard deviation of X, the amount won on a single purchase of a lottery ticket.
On average, over many ticket purchases, the winnings vary by about $44.70
500
Best poster on instagram
Coach Bennett
500
Suppose we know Reid runs normally with a mean of 4.58 minutes in a 1600 and a standard deviation of .42 minutes.
Suppose we know Ben runs normally with a mean of 5.02 minutes in a 1600 and a standard deviation of .28 minutes.
The two boys run a 1600, independently of the other. Find the probability that Reid is faster than Ben. Show work for credit
.8078