Dictionary
Thesaurus Notations
Recipe for Success
Calc (Short for Calculator)
What are the Odds?
Walk the Line
A Sample of Examples
Completely Normal Questions
100
This is a data value that does not fit the overall pattern of the data and also has a large residual
Outlier
100
This represents the mean of a sample
bar x
100
The expression for calculating a residual
y-hat y
100
This is the click path to edit your lists
STAT --> 1:Edit...
100
The probability that you will win in a carnival game is about 1/9. During the last six attempts, you have not won. You decide to give it one last shot. Assuming the outcomes are independent from game to game, the probability that you will win on the next shot is:
1/9
100
Your school counselor wants to see if he can predict a student’s first year college GPA (grade point average) based on their high school graduating GPA. The explanatory variable in this study is?
High school graduating GPA
100
A salmon farmer is curious if a new feed will promote better growth than the current feed. She is also wondering if nutrition level of the water the salmon use could be improved to also promote growth. The farmer assigns 40 fish to 6 different tanks, each having a different combination of 2 salmon food and 3 different nutrition levels of the water. She also assigns 40 fish to a tank with the food and nutrient level used currently on the farm. In this experiment, how many treatments are there?
7 treatments
100
These measures are strongly affected by outliers
Mean and Standard Deviation
Bonus: Range
200
The three numbers 68, 95, and 99.7 are used to describe this rule
The Empirical Rule (for Normal data)
200
This can also be represented as
mu_X
E(X)
200
The equation for calculating a z-sxore
z=(x-mu)/sigma
200
Assuming that your data is already entered in your calculator, this is the click path to find your five number summary for the data
stat --> CALC --> 1:1-Var Stats
200
Event A occurs with probability 0.8. The conditional probability that event B occurs, given that A occurs, is 0.5. The probability that both A and B occur is:
0.4
200
What percent of variability in the cat's body weight is explained by the least-squares regression of body weight on body length?
41.2%
200
Your high school wants to assess their student attitudes towards the new block schedule. The administration randomly selects 5 first block classes out of a possible 35 total first block classes and gives a survey to every student in the class. What type of sample is this an example of?
Cluster
200
For his final AP Statistics project, Daniel wanted to ask the graduating senior class the following questions:
- Will you be attending college?
- What age are you graduating high school at?
- What is your gender?
- What is your graduating GPA?
- What is your phone number?
How many of each variable type are being measured?
3 categorical and 2 quantitative
300
These are the four characteristics that must be discussed when describing a set of data or its distribution.
Shape, Outlier, Center, and Spread
300
This can also be represented as
P(Not A)
P(bar A)
P(A^C)
300
This equation is used when calculating the standard deviation of X given
X~B(n,p)
sigma_X=sqrt(np(1-p)
300
This is the click path you would use if you wanted to calculate an x value for a normal distribution if you know its corresponding area
2nd --> distr --> 3:invNorm(
300
Find the value of k:
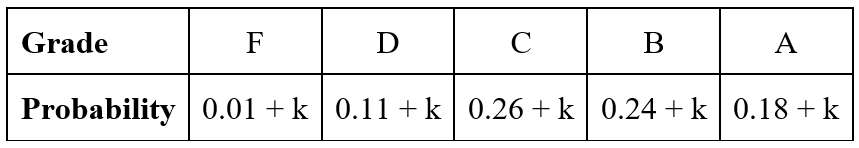
k=0.04
300
Describe the relationship between the correlation coefficients using a compound inequality
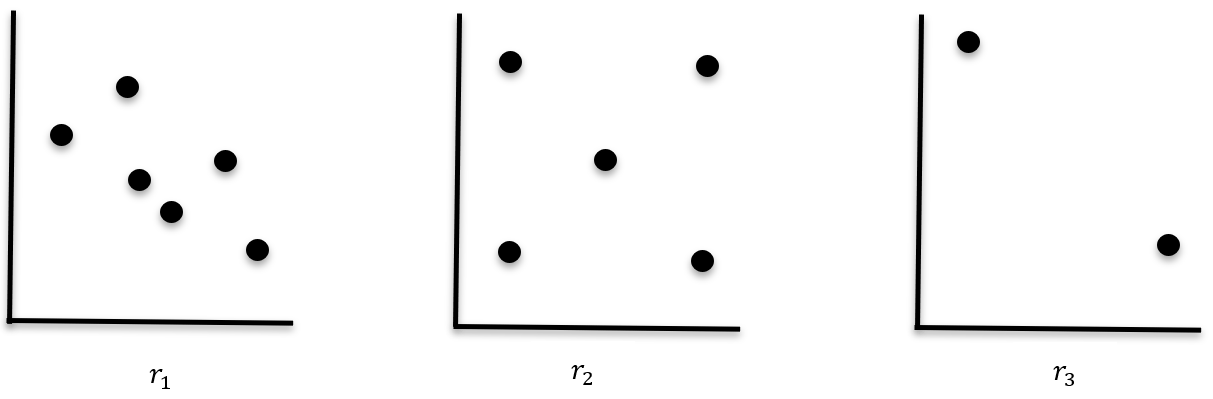
r_3<r_1<r_2
300
You want to draw a sample of 5 unique numbers from a population of 50 numbers. The numbers are labeled 01, 02, . . . , 50, and the line in your table of random digits is:
11362 35692 96237 90842 46843 62719
11 36 23 08 42
300
A variable x follows a normal distribution with a mean of 20 and standard deviation of 5. According to the Empirical Rule, the middle 68% of the data falls between what two x values?
15 and 25
400
Splitting the population into homogeneous group and the selecting an SRS of groups is called this
Stratified Sampling
400
P(X=0)+P(X=1)+P(X=2)+P(X=3)+P(X=4)
P(X<=4)
400
This equation is useful when calculating the probability of A occurring given that B has already occurred.
P(A|B)=(P(AnnB))/(P(B))
400
This is the click path to access this:
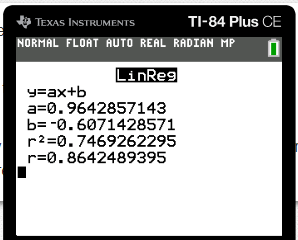
stat --> --> CALC --> 4:LinReg
400
Find the standard deviation of W:
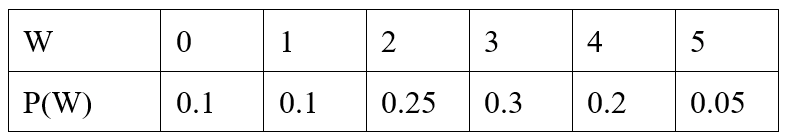
sigma_W=1.32
400
Suppose that the scatterplot of (log x, log y) shows a strong positive correlation. Which of the following must be true?
I. The variables x and y also have a correlation close to 1.
II. A scatterplot of (x, y) shows a strong nonlinear pattern.
III. The residual plot of the variables x and y shows a random pattern.
III only
400
What is the reason for having control groups in an experiment?
To reduce the variability in the results
400
The area under the standard Normal curve corresponding to –0.3 < Z < 1.6 is
0.5631
500
These are the four criteria for good experimental design
Comparison, Randomization, Control, Replication
500
This expression represents a normally distributed set of data
X~N(mu, sigma)
500
This is the equation for calculating the standard deviation for a difference of two random variables X and Y
sigma_(X-Y)=sqrt(sigma_X^2+sigma_Y^2)
500
This is the click path to access the following:
2nd --> list
500
Suppose we have a random variable X where the probability associated with the value
((10),(k))(.37)^k(.63)^(10-k)
What is the mean of X?
mu_X=3.7
500
Find the approximate correlation of the least-squares regression line given:
haty=68.714-0.157x
barx=185.69
bary=39.62
S_x=37.92
S_y=11.09
r~~-0.536
500
Which of the following is (are) important in desgining an experiment?
I. Controling all variables that might have an influence on the response variable.
II. Randomize subjects to treatment groups.
III. Using a large number of subjects to control for small sample variability.
I, II, and III
500
The heights of NFL football players are approximately normally distributed with a mean of 71.5 inches and a standard deviation of 2.3 inches. Aaron Rogers is 6 feet 2 inches. What percentile does that place him at?
86th