What is Sine?
Opposite side of the angle divided by the Hypotenuse
Opposite/Hypotenuse
Find the exact value of the trigonometric function.
cos(π/6)
√3/2
Write each expression in terms of sines and/or cosines, and then simplify.
tan(x)/sec(x)
sin(x)
Evaluate the expression.
sin-1(√3/2)
π/3 radians
Convert the angle in radians to degree.
π/5 radians
36 degrees
State the reference angle for the given angle.
−110°
70°
f(x) = cos(x). Solve f(x) = 12 on [0, 2π).
x = π/3,5π/3
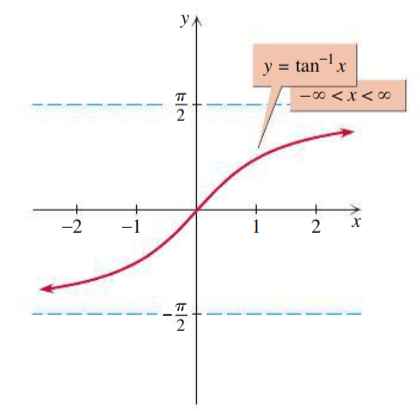
Graph
y=tan-1(x)
Domain:
Range:
Domain:
(−∞,∞)(-∞,∞)
Range:
(−π/2,π/2)
Graph:
Find two positive and two negative angles using radian measure that are coterminal with
π/6
1. 13π/6
2. 25π/6
3. −11π/6
4. −23π/6
If sin(t) = 78 and t is in the 2nd quadrant, find cos(t).
−√15/8
Which of the following equations will shift y=cos(x)
1. 3 units up
2. Amplitude is 2
3. Reflect it about the x-axis
4. to the right
π/6
y=−2cos(x−π/6)+3
Evaluate the expression without using a calculator.
cos(sin-1(3/5))
4/5
Find the exact value of tan x if cos x=-(2/3) and x is not in quadrant III.
tan x =−√5/2
Use the given point on the unit circle to find the value of the sine and cosine of t.

sin(t) = √3/2
cos(t) = −1/2
Write an equation of the form y=Asin[B(x-C)]+D whose graph is the given sine wave.
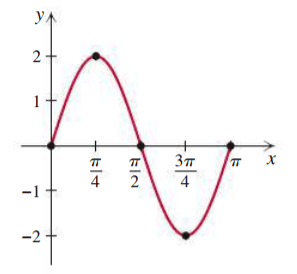
y=2sin(2x)
Use the fundamental identities to simplify the expression.
1 − cos2(x)/tan2(x) + 2 sin2(x)
sin2(x)+1
Find x. (round to the fourth decimal )

146.7314
If tan(t) = 43, and 0 ≤ t ≤ π/2, find the exact values of sin(t), cos(t), sec(t), csc(t), and cot(t).
sin(t)= 4/5
cos(t)= 3/5
sec(t)= 5/3
csc(t)= 5/4
cot(t)= 3/4
Graph one cycle of y=tan(x)
Period:
Domain:
Range:
Asymptotes:
Period:
π
Domain:
(−π/2,π/2)(-π/2,π/2)
Range:
(−∞,∞)(-∞,∞)
Asymptotes:
x=−π/2, x=π/2
Function
(1/1 + cos(x)) − (1/1 − cos(−x)) = −2 cot(x) csc(x)
Prove or disprove the identity.
(1/1 + cos(x)) − (1/1 − cos(−x))=(1/1 + cos(x)) − (1/1 − cos(x))
a.
=(1/1 + cos(x)) · (1 − cos(x)1 − cos(x))− (1/1 − cos(x)) · ( ? / 1+ cos(x))
b.
=1 − cos(x) − ( ? ) / (1 + cos(x))(1 − cos(x))
c.
=−2 cos(x) / 1 − ( ? )
d.
=−2 cos(x) / (?)
e.
=−2 cos(x) / sin(x) · 1 / ( ? )
f.
=−2 cot(x) ( ? )
G.
Is the Function an identity?
a (?)= 1+cos(x)
b (?)= 1+cos(x)
c (?)= cos2(x)
d (?)= sin2(x)
e (?)=sin(x)
f (?)= csc(x)
g. It Is an identity