Is this equation exponential?
h(x)=3x^7-2
NO, the x has to be in the exponent to be considered exponential, the exponent in this case is simply a number.
Find the inverse:
h(x)=(2x+3)/5
h^-1(x)=(5x-3)/2
Simplify
log_(123453145)1
0
Evaluate
log_3(81*243)
9
solve
log(5x-1)=log(x+7)
x=2
Rewrite in logarithmic form
3^7=2187
log_(3)2187=7
Some real estate agents estimate that the value of a house could increase about 4% each year. Write a function to model the growth in value for a house initially valued at $100,000
f(x)=100,000(1.04)^x
Find the inverse of
f(x)=6^x
f^-1(x)=log_(6)x
Simplify
log_(2)32
5
Simplify:
log_(8)80-log_(8)10
1
x=?
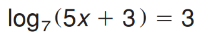
x=68
Evaluate using mental math
log100,000
6
Some real estate agents estimate that the value of a house could increase about 4% each year. A house is valued at $100,000 in 2005. Predict the year its value will be at least $130,000
2012
Find the inverse of
g(x)=sqrt(x^3+1
g^-1(x)=(x^2-1)^(1/3)
Simplify the expression
log_(2)(1/16)
-4
Simplify
log125+log80
4
Solve: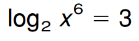
x=sqrt2
Evaluate using mental math
log_(4)256
4
A certain car depreciates about 15% each year. Suppose the car was worth $20,000 in 2010. What is the first year that the value of this car will be worth less than half of that value?
2015
What is the inverse?
y=6^(x/4)
y=log_(6)x^4
Evaluate
log_(16)4
1/2
Evaluate
5log_(4)4-4log_(2)2
1
What value of x satisfies this equation?
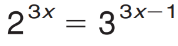
x=0.903
Simplify:
10^(logx)+log_(5)5^x
2x
During the winter months, insects die off at a rate of 2% per week. Assuming the population of insects at a park in Piscataway is 4834, how many insects are left after 16 days?
4616 Insects
What is the inverse of the equation below?
y=(5^x-7)^(1/4)
y=log_(5)(x^4+7)
?
log_(32)128
7/5
Simplify
log_(6)(1/6^4)^3
-12
Solve for the unknown variable.
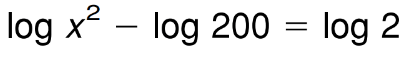
x=+- 20
Show proof: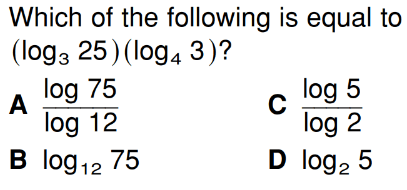
C
This is going to take some voodoo
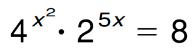
x=(3/10)^(1/3)