Quadratic Quarter Quell
Zero Zero Zero
Boxes???
That Square Root Though
Aye!
200
This is the shape that quadratic graphs look like.
U
200
These are the x-intercepts for this equation:
(x-7)(x+4) = 0
x = 7
x = -4
200
This is the number I would add to both sides to start completing the square:
x^2-8x = 9
+16
200
This is the name for this equation:
x = ((-b ) pm sqrt(b^2-4*a*c))/(2*a)
The Quadratic Formula
200
Defined as this number:
sqrt(-1)
i
300
These are the x-intercepts for this graph:
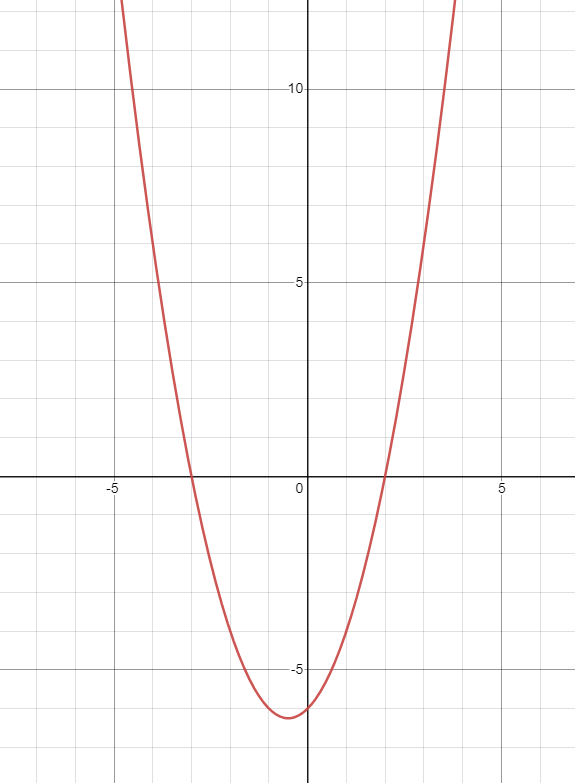
x = -3
x = 2
300
The solutions to this equation:
(2x+3)(4x+1)=0
x = -3/2
x = -1/4
300
This is the perfect square form of the following equation:
x^2-6x+9
(x-3)^2
300
These are the solutions to this equation when you solve using the Quadratic Formula:
x^2-4x+4
x = 2
300
This is the answer to the following equation:
sqrt(-25)
5i
400
The equation for this parabola (in standard form).
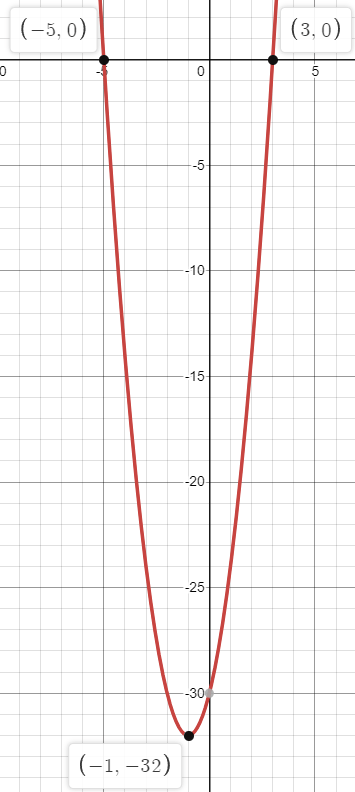
2x^2+4x-30
400
These are the solutions to this equation:
x^2 + 2 x - 15
x = -5
x = 3
400
These are the solutions to this equation when you complete the square:
x^2-4x-12 = 0
x = -2
x = 6
400
These are the solutions to this equation when you solve using the Quadratic Formula:
2x^2+4x-2
x=-1 - sqrt(2)
x=-1 + sqrt(2)
400
This is the answer to the following equation:
(3i)(-5i)
15
500
These are the solutions to this equation.
x^2 + x - 42
x = -7
x = 6
500
These are the solutions to this equation:
x^2 + x - 72
x = -9
x = 8
500
These are the solutions to this equation when you complete the square.
x^2 - 10x - 96 = 0
x = -6
x = 16
500
These are the solutions to this equation when you solve using the Quadratic Formula:
3x^2+2x-12
x = -1/3 - sqrt(37)/3
x = -1/3 + sqrt(37)/3
500
This is the answer to the following equation:
(3i+4)(2i+8)
32i+26