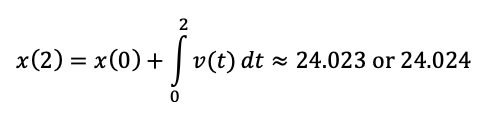What is the antiderivative of cos x?
sin x + C
For the region bounded by y = 4 - x2, y = 0, x = 0 and x = 2, will a left Riemann sum be greater than, less than, or equal to the actual area and why?
greater than the actual area because y = 4 - x2 is decreasing for 0 ≤ x ≤ 2.
∫sin(2x+3)dx=
-1/2cos(2x+3)+C
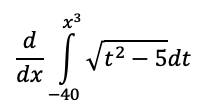
3x^2sqrt(x^6-5)
Brianna is jogging along a straight path. Selected values of her velocity are given in the table below.
Use a right Riemann sum to approximate her displacement for those 40 minutes.
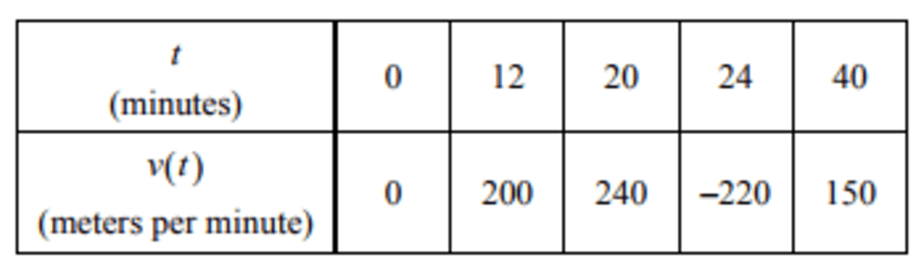
displacement ≈ 12(200)+8(240)+4(-220)+16(150)
= 5840 meters
What is the antiderivative of 2/x?
2ln|x|+C
Use a left-handed Riemann sum to approximate the area between f(x) and the x-axis from x = 0 to x = 10 with widths and function values defined by the table below:

Area ≈ 2(4) + 3(1) + 1(6) + 4(3) = 29
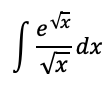
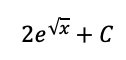
On a Saturday in December, Mrs. Price bakes cookies all day starting at 8 am. If C(t) is her rate of cookie production measured in cookies per hour, and t is measured in hours starting at 8am (t = 0), using correct units, explain the meaning of
∫_0^12 C(t)dt=500
From 8am to 8pm (or from t = 0 hours to t = 12 hours), the total number of cookies Mrs. Price bakes is 500 cookies.
Bob is walking at a velocity modeled by
v(t)=5sin(t^2)
where t is in hours and v(t) is in miles per hour.
Find the total distance Bob traveled from t = 0 to t = 2.
4.924 or 4.925 miles
∫secxtanxdx=
secx + C
Use 4 trapezoids with widths defined by the table below to approximate the area between f(x) and the x-axis from x = 0 to x = 10:
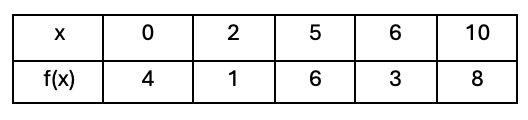
Area≈1/2 [2(4+1)+3(1+6)+1(6+3)+4(3+8)]
=42
∫cot^4(theta)csc^2(theta)d theta
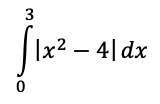
23/3
Bob is walking at a velocity modeled by
v(t)=5sin(t^2)
where t is in hours and v(t) is in miles per hour.
Write and evaluate an integral that would give Bob's average velocity from t = 0 to t = 2.
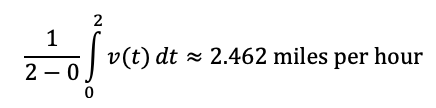
∫(csc^2x+secxtanx)dx=
-cotx+secx+C
Rewrite the integral below using limits
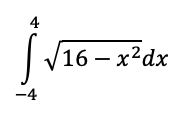
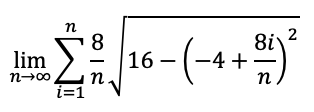
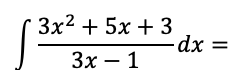
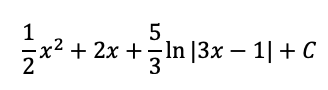
Evaluate the integral below. No calculators. Answer must be fully simplified.
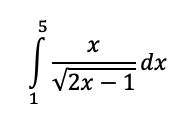
16/3
Bob is walking at a velocity modeled by
v(t)=5sin(t^2)
where t is in hours and v(t) is in miles per hour.
At what time 0 < t < 2 does Bob change direction? JYA
At t ≈ 1.772 hours because v(t) changes sign at t ≈ 1.772
∫3^xdx=
3^x/ln3+C
Rewrite the limit below using integral notation
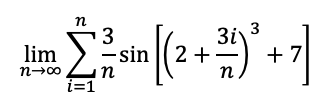
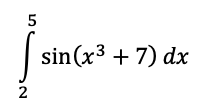
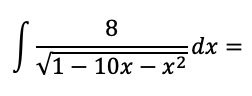
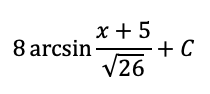
The graph of the continuous function f is below. If
g(x)=2x+∫_-2^x f(t)dt
on what intervals is the graph of g concave down? JYA
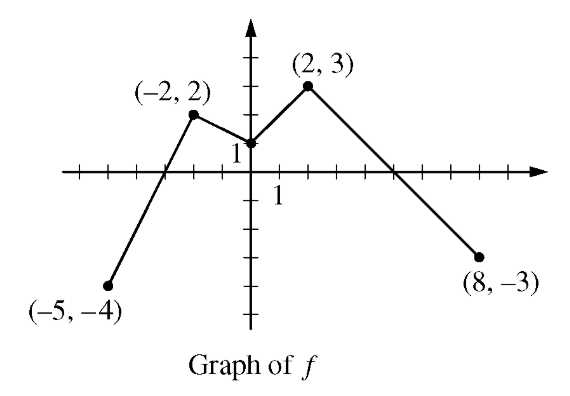
g is concave down on (-2, 0) U (2, 8) because g' = 2 + f(x) is decreasing on these intervals
Bob is walking at a velocity modeled by
v(t)=5sin(t^2)
where t is in hours and v(t) is in miles per hour. Let x(t) be Bob's position function. If x(0) = 20, find x(2).