Find the Critical Points
Graph Questions
First Derivative Test
Particle Motion
100
How do you find critical points from the function?
Take the derivative, find the zeros, and figure out x values you can't plug in.
In a fraction set numerator and denominator equal to zero separately.
100
Given the graph of the first derivative, how do you identify the critical points?
The zeros on the graph
100
What does the sign of f’(x) (i.e. the first derivative) tell you about f?
Increasing or Decreasing
+ -> increasing
- -> decreasing
100
What does the meaning of + and - change to s'(t) for particle motion?
+ is moving right (not inc)
- is moving left (not dec)
200
Find the critical points of
f(x)=3x5-20x3
x=0,2
200
Given the graph of a function, f, how do you identify the critical values?
The maximums, minimums and sharp turns.
200
If f'(x) goes from + to - around a critical point then the critical point is a _______
Relative Maximum
200
What does the meaning of + and - change to s"(t) for particle motion?
+ is slowing down
- is speeding up
300
Find the critical points of
f(x)=(x-1)2 (x+3)
x=1, x=-3, x=0
300
if this is the graph of f'(x) what are the critical points of the original function?
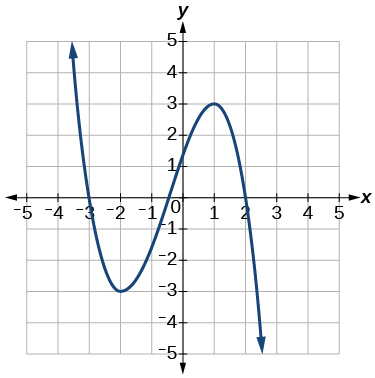
x= -3, -0.5, 2
300
Use the first derivative test to find the relative extrema of the function.
(you may use a calculator, 3 decimal places)
f(x)=3x^4 + 5x^3
relative min (-5/4, -2.441), no max
300
A particle moves along the x-axis with the position function given below. Use a chart to describe the direction of the particle. (Left or Right?)
s(t)=2/3t^3-2t^2
where t>0
moving left from 0 to 2
moving right from 2 on
400
Find the critical points of
f(x)=x^3/(x+5
x= 0, x=-15/2 and x=-5
400
If this is the graph of f'(x) what are the intervals of increase and decrease of the original function?
Increase: (-inf, -3)U(-0.5, 2)
Decreasing: (-3, -0.5)U(2, inf)
400
Use the first derivative test to find the relative extrema of the function
f(x)=1/3x^3+x^2+7
(-2, 25/3) is a relative max
(0, 7) is a relative min
400
A particle moves along the x-axis with the position function given below. Use a chart to describe the direction of the particle. (Left or Right?) Then use the second derivative to describe the speed of the particle.
s(t)=1/3t^3-7/2t^2+12t-5
where t>0
moving right 0 to 3
moving left 3 to 4
moving right 4 on
Speeding up until t=7/2
slowing down after t=7/2