Convert to an improper fraction:
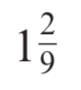
11 / 9
TRUE or FALSE
When + or - fractions, the denominators MUST be the same
TRUE
Fill in the gap
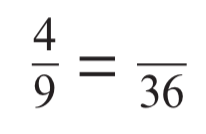
16/36
TRUE or FALSE
When x or ÷ fractions, the denominators MUST be the same
FALSE
The first 3 multiples of 3
3, 6, 9
Convert to an improper fraction: 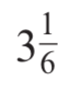
19 / 6
Calculate 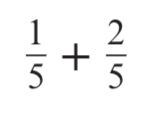
3 / 5
Fill in the gap
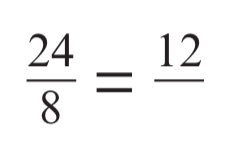
12/4
Calculate:
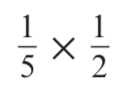
1 / 10
The first 4 multiples of 7
7, 14, 21, 28
Convert to a mixed number:
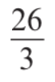
8 2/3
Explain how to get the denominators of two fractions the same
Find a common multiple of both denominators. What ever you do to the bottom of the fraction (x or ÷), you must also do to the top
Fill in the gap 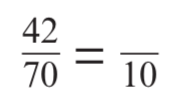
6/10
Calculate: 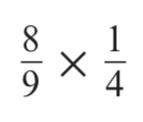
2 / 9
The lowest common multiple of 6 and 12
12
Explain the difference between a proper fraction, improper fraction and mixed number
Proper fraction: numerator < denominator
Improper fraction: numerator > denominator
Mixed number: whole number and fraction
Calculate
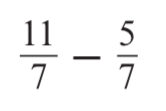
6/7
Explain equivalent fraction
A fraction that has the same value as the original fraction
Calculate: 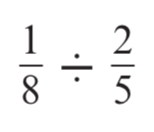
5 / 16
The highest common factor of 12 and 16
4
There are 60 minutes in 1 hour. What fraction of an hour is 17 minutes?
17 / 60
Calculate
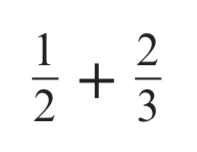
3/6 + 4/6
= 7/6
= 1 1/6
Fill in the gaps 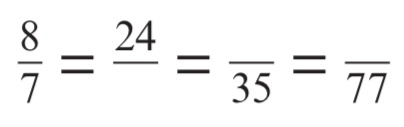
24/21
40/35
88/77
Explain how to ÷ fractions
Step 1: Change the ÷ to a x
Step 2: Turn the second fraction into a reciprocal
Step 3: Proceed like a x problem (simplify vertically or horizontally, multiple the numerators, multiply the denominators, convert improper fractions to mixed numbers where possible)
List the factors of 48
1, 2, 3, 4, 6, 8, 12, 16, 24, 48