Limits
Derivatives
Word Problems
extremas
Concepts
100
Find the limit as x goes to 3 of 2x+6
12
100
Find the derivative if
f(x) = 1/x2 + 12x3 - 80x + Λ
f'(x)= -2/x3 + 36x2 - 80
100
A homeowner wants to have $15,000 available in 5 yrs. Interest is compounded continuously at 6% per year.
What should the homeowner initially put in his bank account?
How fast is it growing in 5 yrs?
1. $11,112.27
2. $900
100
find the relative extremas if MAKE SURE THEY ARE POINTS!!
f(x) = x3+ 3x2 - 9x + 13
r min = (1, 8)
r. max = (-3, 14)
100
what is this?
(f'(x)g(x) - g'(x)f(x))/ (g(x))2
quotient rule
200
Find the limit as h goes to -2 of 4h2-12.
4
200
Find the derivative of s(t) = (2t^2 + 3t + 1)^5
s ' (t) = 5 (2t^2 + 3t + 1)^4 (4t + 3)
200
A population of cells increase at a rate of 5%
according to the continuous exponential growth
Model. There were 2000 to begin with.
Write the equation that models this.
P(t)= 200e^.05t
200
find the point(s) of inflection if
f(x) = x3+ 6x2+10
POI = (-2, 26)
200
write the difference quotient.
(f(x+h) - f(x))/ h
300
Find the limit as x goes to 5 of (x2-3x-18)/(x-6)
8
300
Find the derivative
(x-5)(x+3)
f'(x)= 2x-2
300
Sanrio makes Tuxedo Sam plushies and determines that to sell x amound of plushies they must be priced at p= 90 - 0.4x. The cost to make these plushes are C(x) = 3500 + 0.15 x2. What should the price of the plushies be to maximize profits?
$54.40 
300
Find any critical points and POI in the given interval ( -∞,0 )
f(x)=x3-6x2+36x-10
r max (-6, -226)
300
What is the point of the first derivative test? What about the second derivative test?
first derivative = increasing and decreasing
second derivative = concavity
400
Is f continues at x = 1?
x - 2 x<1
f(x) = x2 + 1 1<=x<3
5/x 3<=x
DNE since left side = -1 and right side = 2
400
Find d/dx
f(x)=x^2/(1-x^2)
f'(x)= 2x/ (1-x^2)^2
400
a pitcher throws a ball in the air. the distance traveled is modeled by
b(t)= t^2+ 6t -80 (I'm sure this is realistic) in ft per seconds
1. what's its velocity at 2 seconds?
2. what's its acceleration at 2 seconds?
1. b'(t)=2t+ 6 [10 ft/s]
2. b''(t) 2 [2 ft/s^2)
400
find any critical points and POI
f(x)= x^3-48-1
(-4,127) max
(4, -127) min
(0, -1) POI
400
What does it mean if elasticity is >1?
The price is inelastic and could be increased to increase profits.
500
find the limit as x approaches 5 if
(x2-25)/(x-5)
as x is approaching 5 lim = 10
500
f(x)= ln(x^2+1)
f'(x) = 2x/(x^2+1)
500
I am about to sell my soul. The cost of selling my soul is modeled by C(s)= s^2+45 in hell coin. The revenue I get from simply existing is modeled by r(s)= 3s^2+30.
Write the Profit equation.
P(s) = (3s^2+30) - (s^2+45) sorry I was too lazy to simplify ∠( ᐛ 」∠)＿
500
Find the critical point(s) if
f(x) = 3x + 20
there are none/ DNE
500
is this a function? Why?
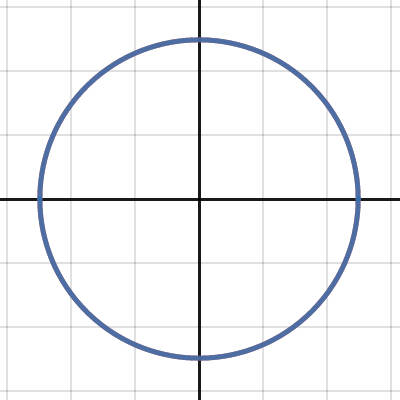
No, it fails the vertical line test :)