Postulates, Theorems and Proofs
Angles
Sequences of Transformations
Coordinate Geometry
Transformations
100
Angles that are opposite and equal
Vertical Angles
100
What is the symbol that describes an angle?
∠
100
What is another name of a sequence of transformations?
A composition of transformations
100
Find Midpoint of (-4,4), (5,-1)
(0.5, 1.5)
100
A transformation that results in proportional sides and congruent angles is a
Dilation
200
Name the Theorem which states that the measure of an exterior angle of a triangle is equal to the sum of the measures of the two remote interior angles.
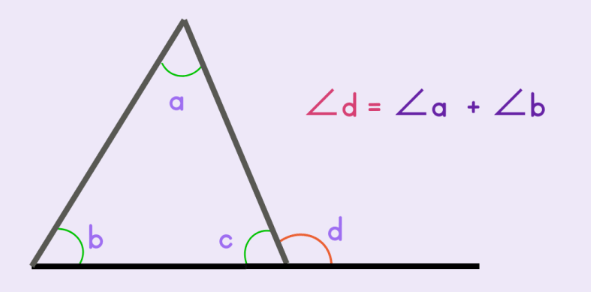
Exterior Angle Theorem
200
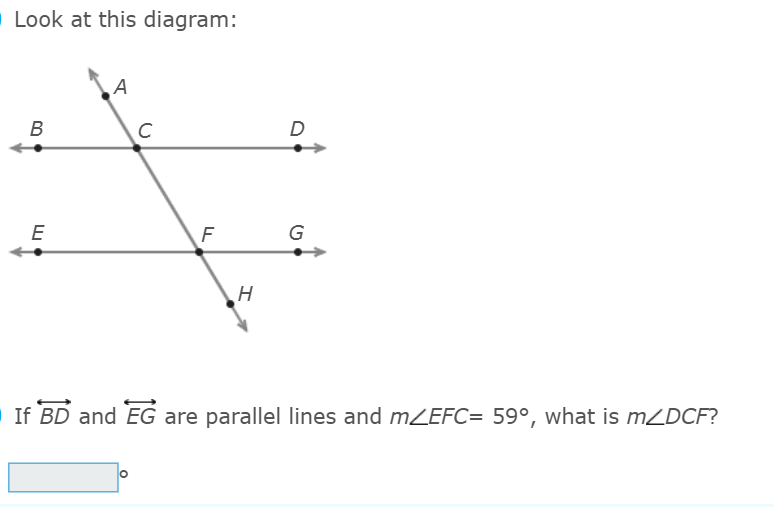
59
200
Which of the following compositions of transformations create congruent figures?
a) A reflection across the y-axis followed by a dilation with a scale factor of 2/3
b) A reflection across the line x=–5, followed by a translation 5 units left and 3 units down.
c) A dilation with a scale factor of 1 followed by a counterclockwise rotation of 90 degrees about the origin
d) A translation 5 units right, 4 units up followed by a dilation at the origin with a scale factor of 3
b and c are correct.
(A dilation with a scale factor of 1 means you multiply each side length by 1, whcih gives the same number😊 )
200
Find distance of (-2,3) and (-7,7).
6.403...
200
An isometry is another name for these types of transformations
Rigid Motions
300
Name the theorem:
The sum of the measures of the interior angles of a triangle = 180 degrees.
Triangle Angle Sum Theorem
300
Which angle does NOT have a measure of 60 degrees?
a) \anglePLB
b) \angleDLM
c) \angleALM
d) \angleLMD
b) \angleDLM
300
Triangle ABC is reflected over the line y=x and then translated by the vector ⟨−4,3⟩. What is the image of point A (2,5) after the sequence?
A'(1,5)
300
Find the number that is three times as far from 2 as it is from 10.
8
300
Which transformation rule applies to the graph?
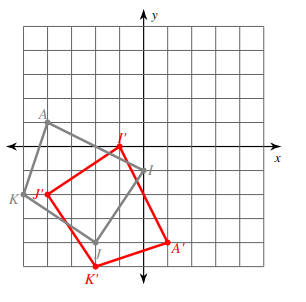
a) Reflections across the line x=2
b) Reflection across the line y=–x
c) Rotation of 180 degrees about the origin
d) Reflection across the line y=x
d) Reflection across the line y=x
400
Which postulate can be used to solve the problem below? Double points for finding the answer
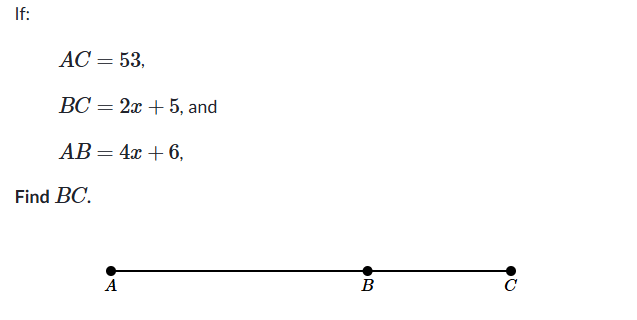
Segment Addition Postulate
BC = 19
400
Find the value of x
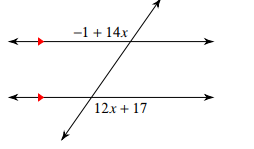
-1+14x=12x+17
14x=12x+18
2x=18
x = 9
400
A figure undergoes a rotation of 90° counterclockwise about the origin, followed by a dilation with scale factor 1/2 centered at the origin. If the original point was (8, -4), what is the final image point?
Rotation of 90 degrees (8, –4) --> (4,8)
Dilation of 1/2: (4/2, 8/2) ---> (2,4)
(2,4)
400
Find the point P that splits the line segment from R (2,1) to S (–8, 6) into a 3:2 ratio.
(–4,4)
400
If Point A is on quadrant II on the coordinate plane. After a 270° clockwise rotation about the origin, in which quadrant is the image located?
Quadrant III
500
Complete the proof
Substitution
500
There are multiple ways to solve this one. Take notes.
x = 8
y = 10
500
When you reflect a figure over the x-axis, then reflect it over the y-axis, this single transformation produces the same result.
A 180 rotation
500
Which of the labeled points splits segment FA into a 4:1 ratio.
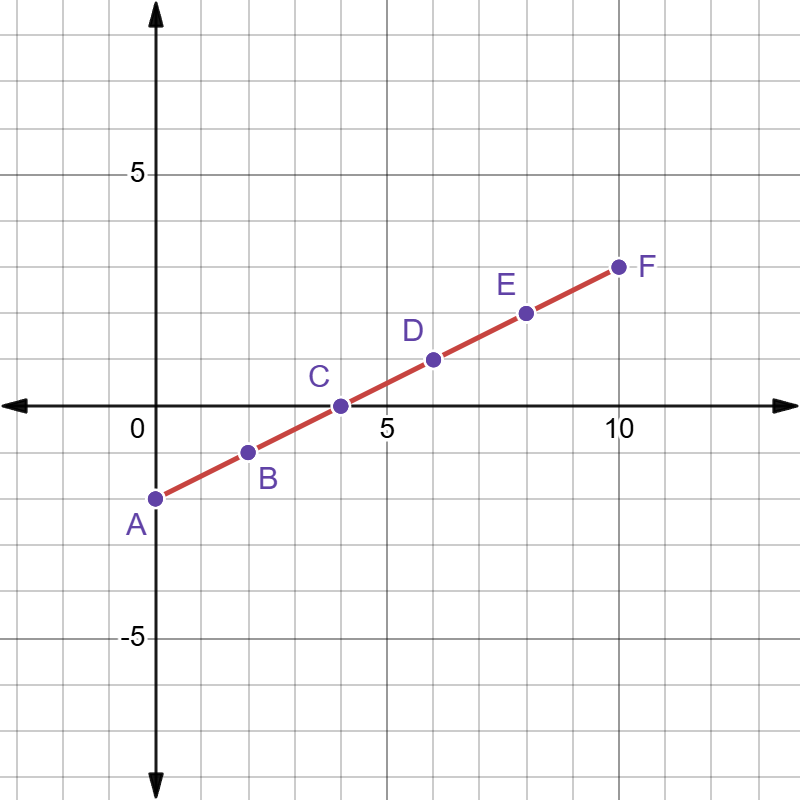
Point B
500
Which transformation can map triangle ABC onto DEF?
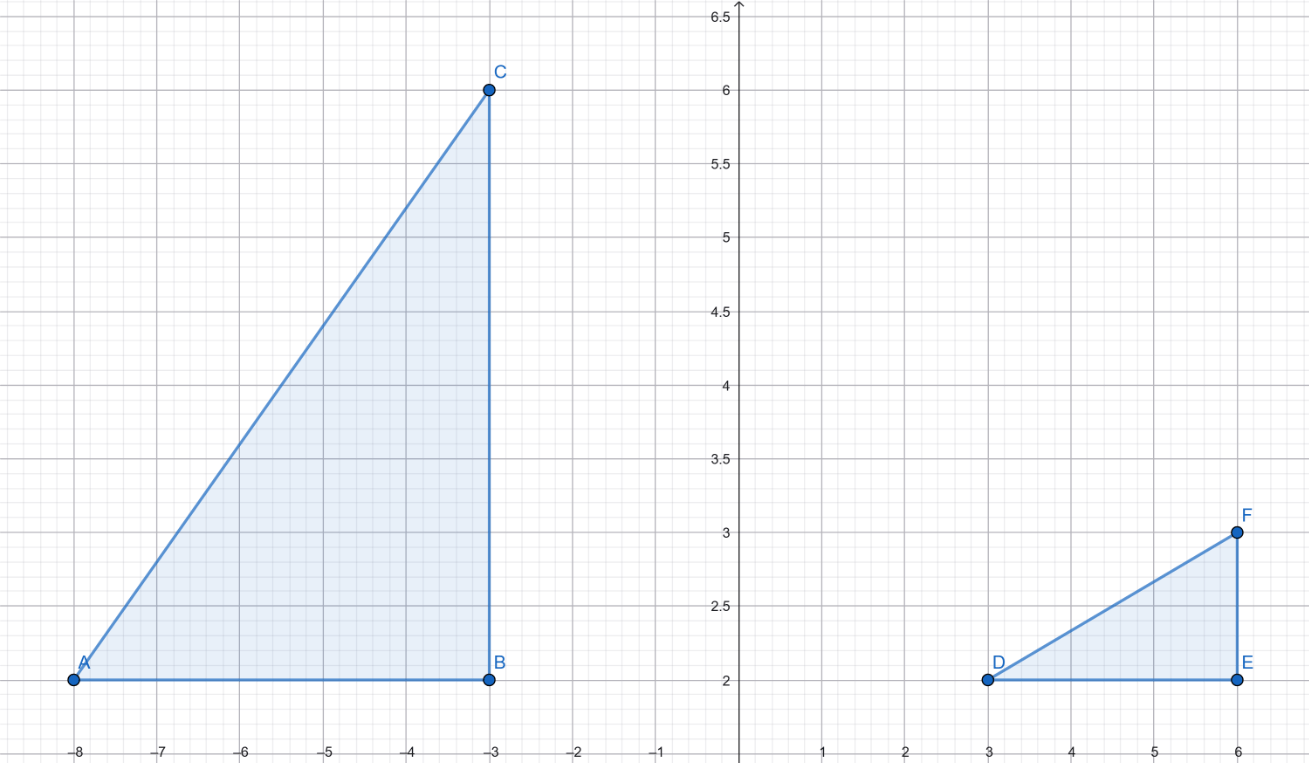
None, the triangles are not congruent nor similar