Binomial Classification
Formulas
Find the Value
Using the Graph
Rounding
100
What does is the acronym BINS used for?
Deciding if a probability setting is Binomial
100
In the calculator prompt binompdf( n , p , x )
What does the n mean?
Number of Trials
100
The probability of a single shot taken on a hockey goaltender being a goal is 8%. Suppose in a typical game, the goaltender has 27 shots against him. Let X be the number of goals in a game.
Find P(X=2) and explain in meaning in context.
P(X=2) = .279
The probability that exactly 2 out of 27 shots are goals in a game is .279
100
What is the shape of a probability distribution for flipping a coin.
Bell/Symmetrical
100
Rewrite 2.45926E-4 using 6 decimal places.
.000246
200
What does the acronym BINS stand for?
Binary
Independent
Numbers
Same Probability
200
In the calculator prompt binompdf( n , p , x )
What does the p mean?
Probability of Success
200
The probability of a single shot taken on a hockey goaltender being a goal is 8%. Suppose in a typical game, the goaltender has 27 shots against him. Let X be the number of goals in a game.
Find P(X < 3) and interpret its value.
P((X < 3) = .833
The probability that at most 3 out of 27 shots are goals in a game is .833
200
Is the probability of success represented in this histogram greater than, less than, or equal to .50?
Less Than
200
Round to three decimal places 4.00356
4.004
300
Owen is trying to predict the Super Bowl coin flip. To collect data, he flips a coin 10 times and record each time he flips Heads.
Is this a Binomial Setting? How do you know?
Binary: Heads or Not Heads
Independent: One Coin Flip Does not impact another
Number: 10 Flips
Same Prob.: 50% Each Time
300
What is the formula for the mean of a binomial distribution?
m=n*p
300
The probability of a single shot taken on a hockey goaltender being a goal is 8%. Suppose in a typical game, the goaltender has 27 shots against him. Let X be the number of goals in a game.
Find the expected value (mean) of X in this situation. Interpret the value.
m=2.16
In a hockey game, we can expect the average amount of goals to be 2.16 out of 27 shots.
300
Which graph is more likely to have a probability of success being .42
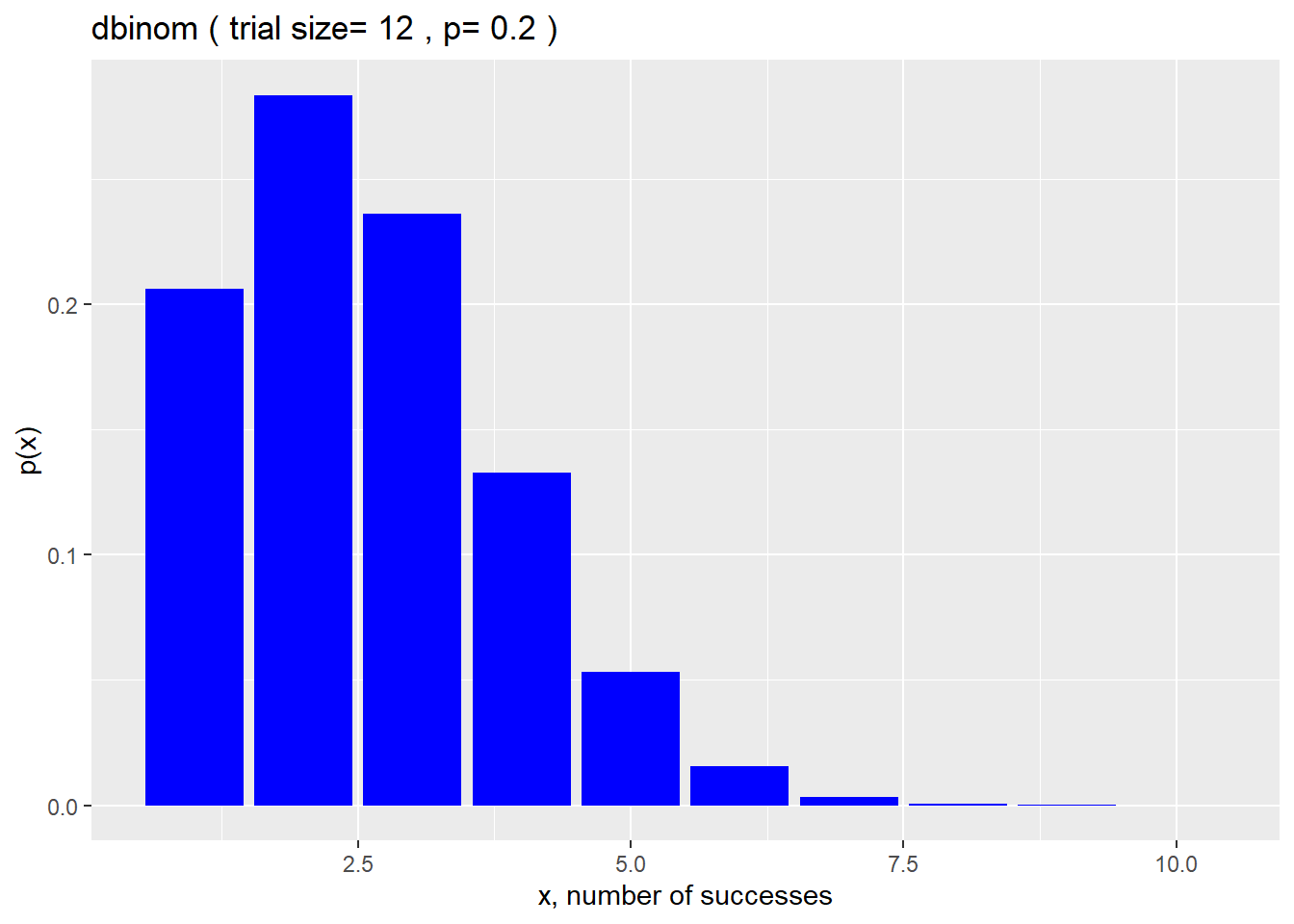
First one (Dark Gray)
300
Round to three decimal places 3.4595894
3.460
400
Addie is making Valentine's Goody-Bags for her friends. She wants to put 2 roses in each bag. She has a dozen roses to choose from and 2 are red, 4 are pink, and 6 are white. She wants to know the probability that both roses in the first bag are pink.
Is this a Binomial Setting? How do you know?
No because the first rose has a 4/12 probability of being pink and the second rose has a 3/11 probability of being pink. The trials do NOT have the same probability.
400
What is the formula for the standard deviation of a binomial distribution?
The square root of (n*p*(p-1))
400
The probability of a single shot taken on a hockey goaltender being a goal is 8%. Suppose in a typical game, the goaltender has 27 shots against him. Let X be the number of goals in a game.
Find the standard deviation of X in this situation. Interpret the value.
St.Dev. = 1.410
The amount of goals per game out of 27 shots, typically differs from the mean by 1.410 goals.
400
What is the shape of a graph with a probability of succuss of .89?
Skewed Left
400
Round to 3 decimal places 8/9
0.889
500
Bobby is planning to go to a Bruins game at TD. He wants to go to a game the the Bruins will win. So he looks at their schedule of up coming games. The Bruins have a 30% chance of beating the Blue Jackets, and 60% chance of beating the Penguins, and a 80% chance of beating the Capitols.
If Bobby picks 1 game to go to, what is the probability that he will see a winning game?
Is this a Binomial Setting? How do you know?
This is not a Binomial Setting because the games do not have the same probability of winning.
500
You roll a six-sided die 10 times.
The chances of rolling a 3 are .167
What is the standard deviation of this binomial setting, where a success is rolling a 3.
The amount of 3's rolled out of ten tries typically differs from the mean by 1.179 rolls.
500
The probability of a single shot taken on a hockey goaltender being a goal is 8%. Suppose in a typical game, the goaltender has 27 shots against him. Let X be the number of goals in a game.
Create a sketch of the probability distribution histogram for this situation.
-Labels Goals/Probability
-x axis labeled 0-27
-Bars that touching/evenly spaced
-Right Skewed (Dramatically)
500
Estimate the probability of success.
.05-.45
500
Round to 3 decimal places 2.99974675
3.000