1.1 Lines in a plane
1.2 Functions
1.3 Graphs and Functions
1.4 Shifting, Reflecting, and Stretching Graphs
1.5 Combinations of Functions
1.6 inverse Function
1.7 Linear Models and Scatter Plots
100
pg.82 #6
Find the slope between the two points
(-2.7,-6.3), (-1,-1.2)
m=(-1.2-(-6.3))/(-1-(-2.7))=5.1/1.7
100
pg 83
#34
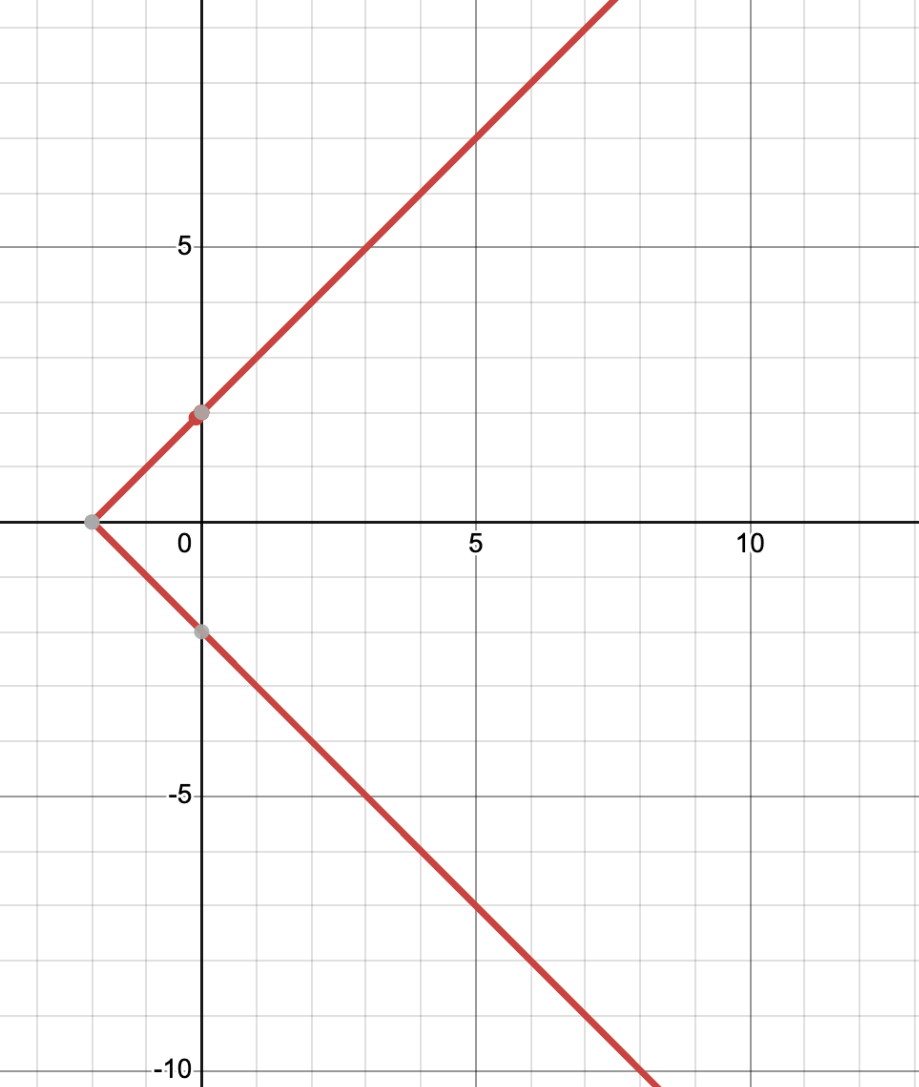
Determine whether the equation represents y as function of x and why?
No because it doesnt pass the vertical line test.
100
pg 83
#51
Find the domain and range algebraically and then use a calculator to check
h(x)=sqrt(36-x^2)
Domain
D: -6<=x<=6
Range
R: y>=0
100
pg 84
#73
identify the common function f(x) and describe the sequence of transformations from f to h
h(x)=x^2-6
shifted down 6
100
pg84
#87Let
f(x)=3-2x
g(x)=sqrt(x)
h(x)=3x^2+2
Find
(f+g)(25)
3-2(25)+sqrt(25)=3-50+5=-42
100
pg 84
#102
Graph the function and using the horizontal line test say whether it has an inverse function.
f(x)=(x-1)^2
It does not pass the horizontal line test and does not have an inverse function
100
pg 84
#109 The following ordered pairs give the entrance exam scores x and the grade point averages y after 1 year of college for 10 students.
(75, 2.3),(82,3)(90,3.6),(65,2)(70,2.1)(88,3.5)(93,3.9)(69,2)(80,2.8)(85,3.3)
Create a scatter plot in your calculator and does a relationship between the two seem linear?
Yep it seems pretty linear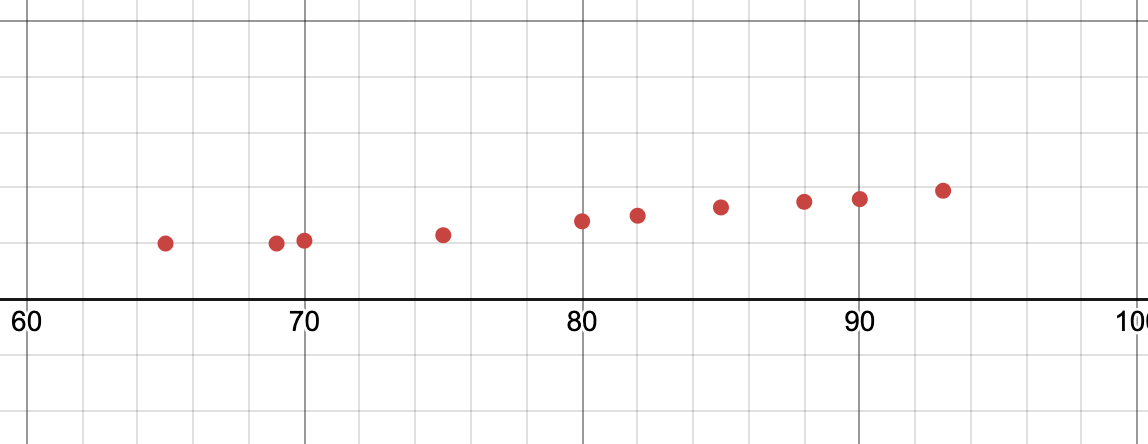
200
pg.82 #20
Find the slope-intercept form of the line that passes through these two points.
Now write it in standard form
(1,6) and (4,2)
m=(2-6)/(4-1)=-4/3
y=-4/3x+b
6=-4/3(1)+b=18/3
22/3=b
Slope intercept Form
y=-4/3x+22/3
3y=-4x+22
Standard Form
4x+3y=22
200
pg 83
#44
Find the domain of the function
f(x)=2/(3x+4)
Domain is anything but x=-4/3
200
pg 83
#57
Using a calculator, determine the intervals the function is increasing, decreasing, or constant
y=x^3-3x
increasing:
-∞->-1 and 1->∞
-∞<x<-1 and 1<x
Decreasing
-1->1 or -1<x<1
200
pg 84
#75
identify the common function f(x) and describe the sequence of transformations from f to h
h(x)=(x-1)^3+7
shifted up 7 and right 1
200
pg84
#89
Let
f(x)=3-2x
g(x)=sqrt(x)
h(x)=3x^2+2
Find
(fh)(1)
(3-2x)(3x^2+2)=9x^2+6-6x^3-4x
-6(1)+9(1)-4(1)+6=5
200
pg 84
#105
Find the inverse function of the given function algebraically
f(x)=x/12
y=x/12
x=y/12
y=12x
f(x)^-1=12x
200
pg 85
#111
In an experiment, students measured the speed s (in meters per second) of a ball t seconds after it was released. The results are shown
Find the line of best fit and estimate the speed of the ball after 2.5 seconds
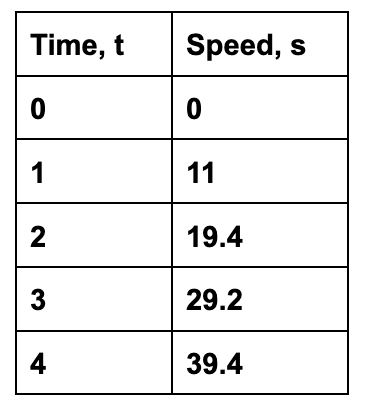
y=9.7x+.4
24.65 m/s
300
pg 82
#25
Write the slope intercept form of the equations to lines through the given point (a) parrallel to the given line and (b). perpendicular to the given line
Point (3,-2)
Line 5x-4y=8
(a) Slope of the line parallel is
5x-4y=8
5x-8=4y
5/4x-2=y
Slope is 5/4 no to find the line plug point into the equation
y=5/4x+b
-2=5/4(3)+b
-8/4-15/4=b=-23/4
y=5/4x-23/4
(b) same but now the slope is the opposite reciprocal
m=-4/5
y=-4/5x+b
-2=-4/5(3)+b
-10/5+12/5=b=2/5
y=-4/5x+2/5
300
pg 83
#45
A hand tool manufacturer produces a product for which the variable cost is $5.35 per unit and the fixed costs are $16,000. The company sells the product for $8.20 and can sell all that it produces.
(a) Write the total cost C as a function of x, the number of products produced.
(b)Write the profit P as a function of x
(a)
C=5.35x+16000
(b)
P(x)=-5.35x+8.2x-16000
300
pg 83
#64
Using a calculator, approximate to two decimal places, any relative minimum or maximum values.
y=x^{3}-4x^{2}-1
Relative maximum (0,-1)
Relative Minimum (2.67,10.48)
300
pg 84
#81
identify the common function f(x) and describe the sequence of transformations from f to h
h(x)=-2x^2+3
shifted up 3 and stretched vertically steeper by 2, flipped over the x axis
300
pg84
#91
Let
f(x)=3-2x
g(x)=sqrt(x)
h(x)=3x^2+2
Find
(h∘g)(7)
(h∘g)(7)=h(g(7))
g(7)=sqrt(7)
h(g(7))=3(sqrt7)^2+2=21+2=23
300
pg 84
#107
Find the inverse function of the given function algebraically
f(x)=4x^3-3
y=4x^3-3
x=4y^3-3
(x+3)/4=y^3
root(3)((x+3)/4)=y=f(x)^-1
300
The table shows the sales S (in millions of dollars) for Timerland from 1995 to 2002.
Find the line of best fit and when sales will exceed $1300 million
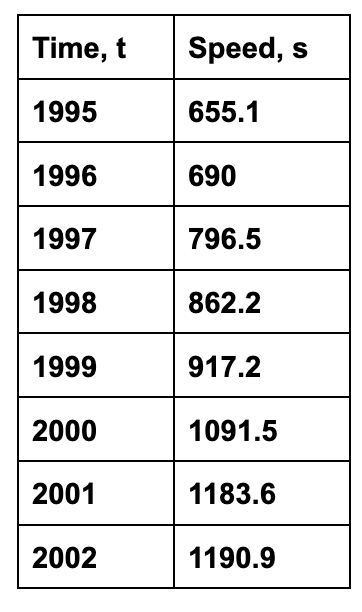
y=85.22x+198.99
year 13 which is 2003 it will exceed $1300 million