The answer to (8+4i)-(6+5i).
What is 2 - i?
(8+4i)-(6+5i) = 8 + 4i - 6 - 5i = 2 - i.
The quadratic function
f(x) = a(x-h)^2+ k, a !=0,
is in ____ form. The graph of f is called a/an ____ whose vertex is the point ____. The graph opens upward if a ____ and opens downward if a ____.
What is
"The quadratic function is in standard form. The graph of f is called a parabola whose vertex is the point (h,k). The graphs opens upward if a is positive and opens downward if a is negative."
The degree of the polynomial function f(x) = -x3(4x+2)(x-7) is _____. The leading coefficient is _____.
What is "degree of 5" and "leading coefficient of -4?"
For the degree, add the exponents of x together. For the leading coefficient, multiply the first factors only.
When using synthetic division to perform the following operation, this is the number you divide by.
(4x^3-3x^2+3x-1)-:(x-1).
What is 1?
The Rational Zero Theorem states that if p/q is a rational zero of f, (where p/q is reduced to lowest terms), then p is a factor of ____ and q is a factor of ____.
What is "p is a factor of the constant and q is a factor of the leading coefficient?"
The domain of
f(x) = (x+3)/(x^2-4)
What is all real numbers except for x=2 and x=-2 or
(- oo,-2)uu(-2, 2)uu(2,oo)
The boundary points for (x+4)(x-7)>0.
What is x=-4 and x=7?
The product of (-7+4i)(2 - 5i).
What is 6 + 43i?
(-7+4i)(2 - 5i) = -14 +35i + 8i - 20i2
= -14 + 43i -20(-1) = -14 + 43i + 20
= 6 + 43i
The coordinates of the vertex for
f(x) = -2(x+1)^2 + 5
What is (-1, 5)?
Use the leading coefficient test to determine the end behavior of the following function:
f(x) = -7x^4 + 3x^3-6x^2-x+2
What is "the graph falls to the right and falls to the left?"
Since the leading coefficient (-7) is negative, the right side falls.Since the degree (4) is even, both ends go in the same direction.
Use synthetic division to find the quotient of the following problem.
(4x^3-3x^2+3x-1)-:(x-1)
What is
4x^2 + x + 4 + 3/(x-1)
Use the Rational Zero Theorem to list all possible rational zeros of the following function.
f(x) = 4x^3 + 5x^2-3x + 10
What is
+-{1,2,5,10,1/2,1/4,5/2,5/4}
pm {(1,2,5, 10)/(1,2,4)} = +-{1,2,5,10,1/2,1/4,5/2,5/4}
Find any vertical asymptotes or holes for the following function:
f(x) = (x^2-36)/((x+6)(x-2)
What is a vertical asymptote at x=2 and a hole at x=-6 or (-6, 3/2)?
Solve the inequality below and state the answer in interval notation.
(x+4)(x-7)>0
What is
The result in standard form of
(5i)/(3+2i).
What is
10/13 + 15/13 i?
(5i)/(3+2i) *(3-2i)/(3-2i) = (15i-10i^2)/(9-4i^2) = (15i-10(-1))/(9-4(-1)) = (10+15i)/(13)= 10/13 + 15/13 i.
When a function is in the form f(x) = ax^2+bx+c, you can use the formula x=(-b)/(2a) to find the x-coordinate of the vertex. Find the vertex of
f(x) = 2x^2 + 4x - 3.
What is (-1, -5)?
x= -b/(2a) = -4/(2*2) = -4/4 = -1
y=2(-1)^2+4(-1)-3 = 2-4-3=-5
Find the zeros of the following function and give the multiplicity of each zero. State whether the graph crosses the x-axis or touches the x-axis and turns around, at each zero.
f(x) = 4(x-7)^2(x+4)^3(x-1)
What is...
"zero at x=7, multiplicity of 2, touches the x-axis and turns around;
zero at x=-4, multiplicity of 3, crosses the x-axis;
zero at x=1, multiplicity of 1, crosses the x-axis."
Use long division to find the quotient of the problem below.
(6x^3+7x^2+12x+5)-: (3x-1)
What is
2x^2 + 3x + 5 +10/(3x-1)?
Which of the following values could be possible rational zeros of
f(x) = x^3-4x^2-7x+10?
x= -3, -2, -1, 0, 1, 2, 3
What is x= -2,-1, 1, and 2?
Horizontal asymptotes:
If the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is ____.
If the degree of the numerator is the same as the degree of the denominator, the horizontal asymptote is _____.
If the degree of the numerator is greater than the degree of the denominator, the horizontal asymptote is _____.
What is y=0, y=a/b, and none?
Solve the inequality below and express the solution in interval notation.
3x^2+ 10x - 8 <= 0
What is
[-4, 2/3] ?
3x^2+ 10x - 8 <= 0
Turn inequality into an equation, factor, and solve for x for the boundary points. (3x -2)(x+4)=0
x=2/3, x=-4 Now mark these values on a number line and test points on each side and in between to see when the values are less than or equal to 0 (negative values).
The result of
(3sqrt-5)(-4 sqrt -12)
What is
24 sqrt15
(3sqrt-5)(-4 sqrt -12) = (3i sqrt5)(-4i sqrt12)= (3i sqrt5)(-4i*2 sqrt3) = (3i sqrt5)(-8i sqrt3) = -24i^2 sqrt15 = -24(-1) sqrt 15 = 24 sqrt15
Without graphing, determine if the following function has a minimum or maximum and state where it occurs.
f(x) = 3x^2 - 12x - 1
What is a minimum at (2, -13)?
x = -b/(2a) = -(-12)/(2*3) = 12/6 = 2
y=3(2)^2 - 12(2) - 1 = 12-24-1=-13
Find the zeros for the following function and give the multiplicity for each zero. State whether the graphs crosses the x-axis, or touches the x-axis and turns around, at each zero.
f(x) = x^3+7x^2-4x-28.
What is...
"zero at x=-7, multiplicity of 1, crosses the x-axis;
zero at x=-2, multiplicity of 1, crosses the x-axis;
zero at x=2, multiplicity of 1, crosses the x-axis."
f(x) = x^3+7x^2-4x-28 = (x^3+7x^2)+(-4x-28)=x^2(x+7)-4(x+7) = (x+7)(x^2-4)=(x+7)(x+2)(x-2)
Find the answer to the following problem:
(18x^4+9x^3+3x^2) -: (3x^2+1)
What is
6x^2+3x-1- (3x-1)/(3x^2+1)
When trying to factor a higher-degree polynomial and factoring is not obvious, you can begin with listing the possible rational zeros. Once p/q values are found, use a graphing calculator to verify at least one rational zero. After an x-intercept is identified, then use _________ to simplify the polynomial into a lower-degree polynomial that may be factorable.
What is synthetic division?
Find the vertical and horizontal asymptotes for the following function:
f(x) = (x^3+2x^2-3x)/(x^2-9x+8)
What is a vertical asymptote at x=8 and no horizontal asymptote?
f(x) = (x^3+2x^2-3x)/(x^2-9x+8) = (x(x^2+2x-3))/((x-1)(x-8)) = (x(x+3)(x-1))/((x-1)(x-8)) = (x(x+3))/(x-8)
Since the degree of the numerator (3) is larger than the degree of the denominator (2), there is no horizontal asymptote.
Use the following graph to solve this inequality:
x2 -2x - 8 >0
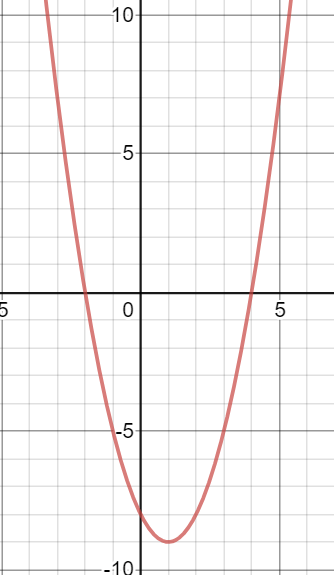
What is
(-oo, -2)uu( 4, oo)?
x2-2x-8=0
(x-4)(x+2)=0
x-4=0 x+2=0
x=4 x=-2 These are the boundary points.
Now look at the graph and see which intervals have positive y-values.
Solve using the quadratic formula and express the answer in standard form.
3x^2 = 8x - 7
What is
4/3 +- i sqrt5/3?
3x^2 - 8x + 7 = 0
x=(-b pm sqrt (b^2-4ac))/(2a)
x=(-(-8) pm sqrt ((-8)^2-4(3)(7)))/(2(3)
x=(8 pm sqrt (64-84))/6
x=(8 pm sqrt (-20))/6)
x=4/3 pm i (sqrt5)/3
A ball is thrown upward and outward from a height of 6 feet. The height of the ball, f(x), in feet, can be modeled by the following function where x is the ball's horizontal distance, in feet, from where it was thrown. What is the maximum height of the ball and how far from where it was thrown does this occur?
f(x) = -0.8x^2 + 2.4x + 6
What is "the maximum height is 7.8 feet that occurs 1.5 feet from where it was thrown?"
x=-b/(2a) = - 2.4/(2(-0.8))= -2.4/-1.6 = 1.5
y=-0.8(1.5)^2 + 2.4(1.5) + 6 = 7.8
Use the Intermediate Value Theorem to show that the polynomial has a real zero between the given integers.
f(x) = x^3 + x^2 -2x + 1
between-3 and -2.
What is ...
f(-3) = (-3)^3 + (-3)^2 -2(-3) + 1 = -27+9+6+1=-11
and
f(-2) = (-2)^3 + (-2)^2 -2(-2) + 1=-8+4+4+1= 1
Since f(-3) is negative and f(-2) is positive, there must exist an x-intercept between these two x-values.
Solve the equation below given that 2 is a zero.
f(x)=2x^3-5x^2+x+2=0
What is x=2, -1/2, and 1?
Use synthetic division using x=2 to get 2x^2-x-1=0. From there factor into (2x+1)(x-1)=0 and solve for x to get the other two solutions of -1/2 and 1.
Find the three solutions of x^3-10x-12=0 using the Rational Zero Theorem, synthetic division, and the quadratic formula. Give exact solutions.
What is
x=-2, 1+ sqrt7, and 1- sqrt 7
A tourist drives 90 miles along a scenic highway and then takes a 5-mile walk along a hiking trail. The average velocity driving is nine times that while hiking. Express the total time for driving and hiking, T, as a function of the average velocity on the hike, x.
What is
T(x) = 10/x + 5/x?
Distance equals velocity times time. D = vt
Driving: 90 = (9x)t Hiking: 5 = xt
Driving: t = 90/(9x) = 10/x Hiking: t = 5/x
Total time is 10/x + 5/x.
Solve the inequality and state the answer in interval notation:
abs(x^2+2x-36)>12.
What is
(-oo,-8)uu(-6, 4)uu(6, oo)?
First set the absolute value problem equal to twelve.
abs(x^2+2x-36)=12.
Write the two equations for this absolute value problem and solve for x.
x^2+2x-36=12 and x^2+2x-36= -12
Set each equation equal to 0, factor, and solve for x.
x^2+2x-36=12 => x^2+2x-48=0=>(x+8)(x-6)=0=>x=-8, 6
x^2+2x-36= -12 =>x^2+2x-24=0 => (x+6)(x-4)=0 => x=-6, 4
Mark each boundary point on a number line and use test points to find where the original problem is true.