Continuity
Limits at a Value
Limits at Infinity
Derivatives
Applications of Derivatives
100
Sketch a graph with the following characteristics:
-removable discontinuity at x = -4
-f(-4) = 3
-jump discontinuity at x = 2
-infinite discontinuity at x = 5
Answers vary
100
lim_(x->-1) (2x^2 + 3x + 1)/(x^2 - 2x - 3)
1/4
100
lim_(x->-oo)(4x^3 + 6x^2 - 2)/(2x^3 - 4x + 5)
2
100
In the graph below, determine which line represents f, f', f'' .
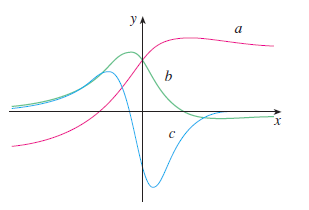
f = a, f' = b, f'' = c
100
Fine the slope of the tangent line to the curve
y = x - x^3
at the point (1, 0).
m = -2
200
Determine the values at which the follow function is not continuous. Describe the type of discontinuity and provide mathematical justification for why the discontinuity exists.
f(x) = (2x^2-7x - 15)/(x^2 - 6x + 5)
x = 5, removable discontinuity
f(5) DNE
x = 1, infinite discontinuity
f(1) DNE or lim_(x->1)f(x) DNE
200
lim_(x->2) (sqrt(4x + 1) - 3)/(x - 2
2/3
200
lim_(x->-oo)-4x^2 + 7x^5 - 3x + 6
-oo
200
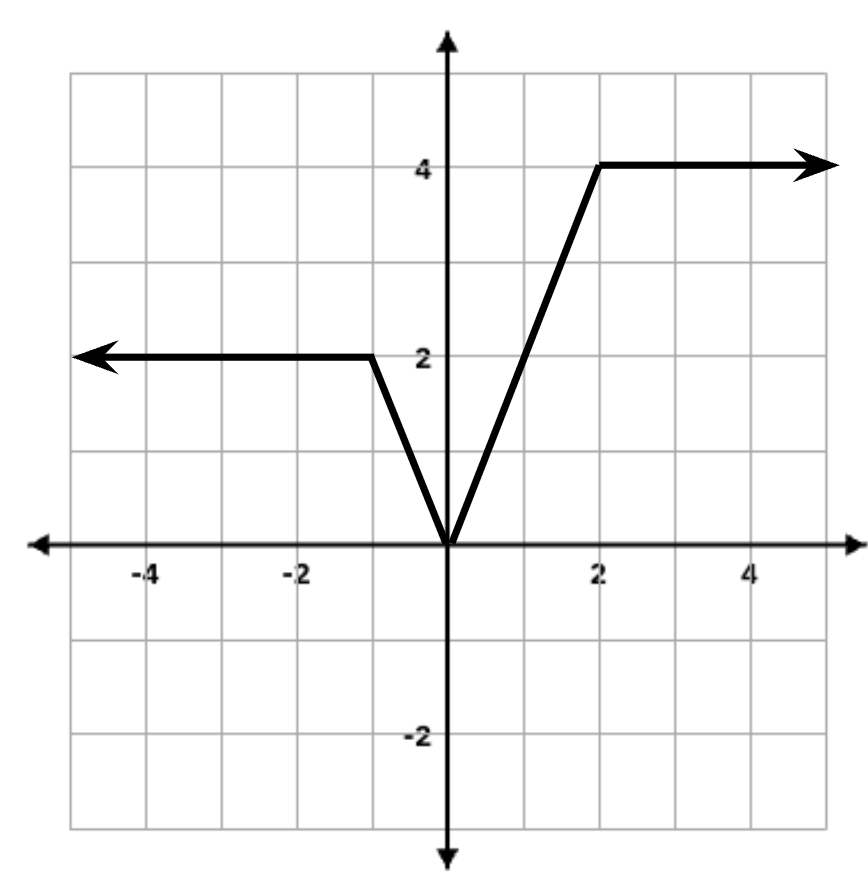
The graph below is f(x). Sketch f'(x).
200
Find the equation of the tangent line to the curve represented by the function below when x = 1
g(x) = x^4 - 2
y+1 = 4(x -1)
y = 4x - 5
300
Determine the numbers at which f(x) is discontinuous and what type of discontinuity exists.
f(x) = {(2^x if x <= 1), (3 - x if 1 < x <= 4), (sqrt(x) if x>4) :}
jump discontinuity at x = 4
300
lim_(x->0) ((1/(x + 5)- 1/5)/x)
-1/25
300
Evaluate the following limit using Squeeze Theorem. Make sure to show all work
lim_(x->oo)sinx/x
-1/x <= sinx/x <= 1/x
lim_(x-> oo)(-1/x) = 0
lim_(x-> oo)(1/x) = 0
lim_(x-> oo)(sinx/x) = 0
300
Find f'(a) using the limit definition (use x->a approach).
f(x) = 2x^3 + x
f'(a) = 6a^2 + 1
300
The displacement, in feet, of a particle moving in a straight line is given by the following function, where t is time in seconds. What is the instantaneous velocity when t = 8?
s = 1/2t^2 - 6t + 23
2 ft/sec
400
Use the Intermediate Value Theorem to show that there is a root of the given equation in the specified interval. Make sure you include everything in your explanation!
lnx= x - sqrt(x), (2, 3)
The equation
ln(x) - x +sqrt(x) = 0
is continuous over the interval [2, 3] because log functions, root functions, and linear functions are continuous within their domains. The domain of ln(x) is (0, inf) and the domain of sqrt(x) is [0, inf). f(2) = 0.107, f(3) = -0.169. Since f(3)<0<f(2), there exists a value, c, such that f(c) = 0 by IVT in the interval (2, 3)
400
Evaluate the limit of the function below, f(x). If the limit DNE, explain why and be specific!
lim_(x->4)(x^2 + 3x)/(x^2 - x - 12)
DNE because...
lim_(x->4^-)f(x) = -oo
lim_(x->4^+)f(x) = +oo
lim_(x->4^+)f(x) != lim_(x->4^-)f(x)
400
lim_(x->-oo)(sqrt(4x^2 + 3x) + 2x)
-3/4
400
Find f'(a) using the limit definition (use h->0 approach)
f(x) = x^-2
f'(a) = -2/a^3
400
A particle moves along a straight line as modeled below, with s measured in meters and t in seconds. Find the velocity when t = 4.
s = 10 + 45/(t + 1)
-9/5 m/sec
500
Find the values for a and b that make f continuous everywhere.
f(x) = {((x^2 - 4)/(x - 2) if x<2), (ax^2 - bx + 3 if 2<=x<3), (2x - a + b if x>=3):}
a = b = 1/2
500
Find the limit of the function below, f(x). If it does not, explain why. Be specific!
lim_(x->-6) (2x + 12)/abs(x + 6)
DNE because
lim_(x->-6^+)f(x) = 2
lim_(x->-6^-)f(x) = -2
lim_(x->-6^-)f(x) != lim_(x->-6^+)f(x)
500
lim_(x->-oo)sqrt(1 + 4x^6)/(2 - x^3)
2
500
Find f'(a) using the limit definition (use h->0 approach).
f(x) = sqrt(1-2x)
f'(a) = -1/sqrt(1-2a)
500
An alien on Mars picks up a rock and throws it. The height of a rock, in meters, after t seconds is modeled with
h(t) = 10t - 2t^2
What is the velocity of the rock when it hits the ground? Hint: find the time when the rock hits the ground first!
-10 m/sec