Modeling with Differential Equations
Slope Fields and Euler's Method
Separable Differential Equations
Exponential and Logistic Growth
100
A calculus student's motivation M is decreasing at a rate equal to the amount of time t since lunch. This is a differential equation modeling the situation.
What is (dM)/dt = -t ?
100
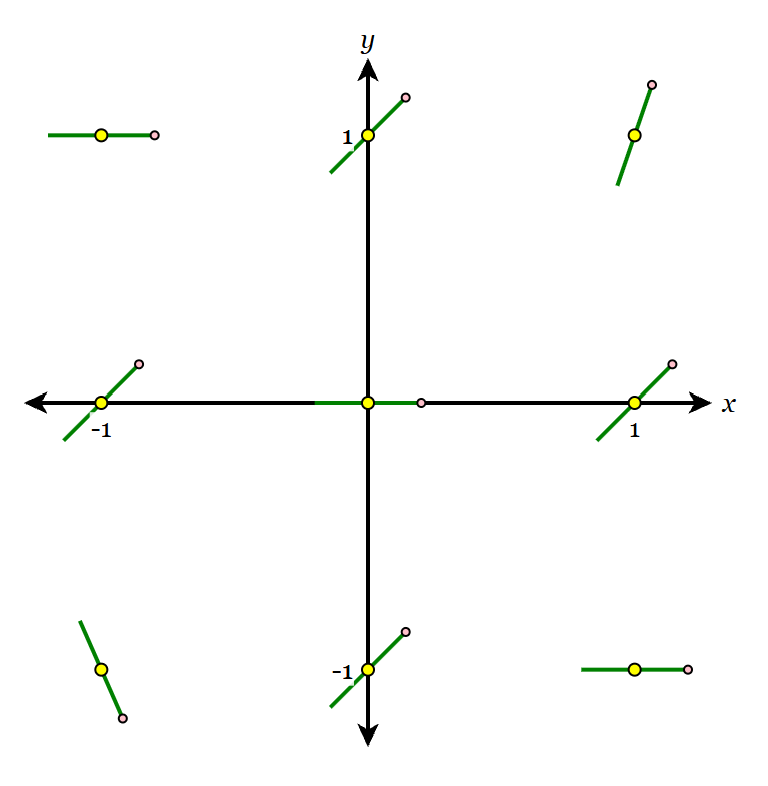
Draw a slope field at the indicated points for the differential equation dy/dx = x+y 
100
This is the general solution to the differential equation dy/dx = x^2/y^2.
What is y=x+C ?
100
This is the general formula for the size of a population P(t) which satisfies P(0)=P_0 is increasing at a rate (dP)/dt=kP.
What is P(t)=P_0e^{kt) ?
200
A dripping faucet is filling a sink with a 10 gallon capacity. The volume V of the water in the sink is increasing at a rate equal to the difference between the capacity of the sink and the current volume of water. This is a differential equation that models the situation.
What is (dV)/dt = 10-V ?
200
The differential equation matching the given slope field is:
A) dy/dx = -y^2/(x-1)
B) dy/dx = y/(x-1)^2
C) dy/dx = -(x-1)/y^2
D) dy/dx = -(x-1)y^2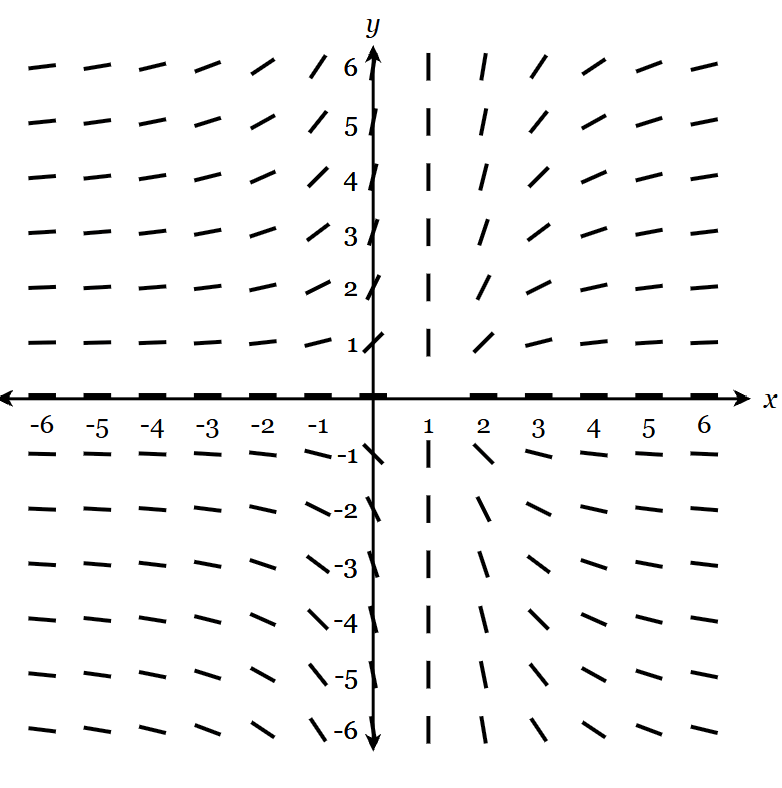 
What is B?
200
This is the particular solution y=f(x) to the differential equation dy/dx=x^2/(2y) satisfying f(3)=3.
What is y=sqrt(x^3/3) ?
200
This is the general formula for the population P(t) which is growing at a rate (dP)/dt=kP(1-P/M) and has an initial population of P_0.
What is
P(t)=M/(1+((M-P_0)/P_0)e^(-kt))?
300
The area A of a leaf is increasing at a rate that is two less than 7 times the square of the amount of sunlight l that it receives. This is a differential equation that models the situation above.
What is (dA)/(dl) = 7l^2-2 ?
300
Let f(x) be a function satisfying f(-1)=1. Selected values of the derivative of f(x) are given in the table below:
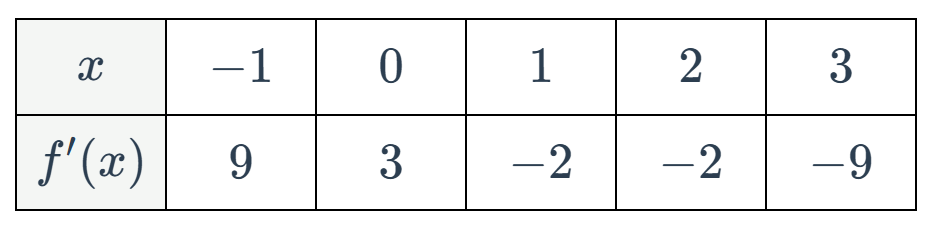
This is the approximation for f(3) obtained by using Euler's method with two steps of equal size starting at x=-1.
What is 15?
300
This is the particular solution to the differential equation dy/dx = (x^2-5)/(2y^2) satisfying the initial condition y(-3)=3.
What is y=((x^3-15x+36)/2)^(1/3) ?
300
A population grows at a rate (dP)/dt=P/200(10-P). This is the value of P at which P(t) has an inflection point.
What is P=5 ?
400
The volume V of a tank being filled with water increases at a rate which is directly proportional to the amount of time t that has passed. This is an example of a differential equation that could model the situation.
What is (dV)/dt = kt ? (Any value of k is acceptable).
400
Let y=f(x) be the solution to the differential equation dy/dx = x-3y+1 satisfying f(6)=-2. This is the approximation for f(16) obtained by using Euler's Method with two steps of equal sizes, starting at x=6.
What is -822?
400
This is the particular solution to the differential equation dy/dx=cos(x)y with the initial condition y((3pi)/2)=e.
What is e^(sin(x)+2) ?
400
This is the particular solution to the exponential differential equation (dP)/dt=kP satisfying P(0)=3 and P(10)=45.
What is P(t)=3e^((ln15/10)t) ?
500
A balloon is being inflated by a pump with pressure p. After t seconds, the volume V is increasing at a rate that is directly proportional to the product of the pressure and the natural log of the volume and inversely proportional to the square of the difference between t and the cosine of the natural log of the pressure. This is a differential equation that models the situation above.
What is (dV)/dt = (kpln(V))/(t-cos(ln(p)))^2 ? (Any value of k is acceptable).
500
Let y=f(x) be the solution to the differential equation dy/dx=xy satisfying f(2)=3. This is the approximation of f(23) obtained by using Euler's Method with three steps where each successive step is twice the size of the previous step.
What is 86583 ?
500
This is the particular solution to the differential equation dy/dx=(sinxcosx)/(ycosy) which passes through the point (-pi/2,pi). The answer may be left in implicit form rather than solved explicitly for y.
What is ysiny+cosy=(sin^2x)/2-3/2 ?
500
This is the particular solution to the differential equation (dP)/dt=-P^2/3+210P satisfying P(0)=7 and P(3)=70.
What is P(t)=630/(1+89e^(((ln(89/8))/3)t)) ?