Take it to the Limit
Warning: Contains Implicit Material
It's Critical
Deriv Applications
You get the graph!
These are triggy
100
lim_(x->4) (x^2-7x+12)/(x-4)
1
100
If 2x^2+5y^2-2xy=5
(dy)/(dx)=
(2y-4x)/(10y-2x)=(y-2x)/(5y-x)
100
Find the critical values of
f(x)=2x^3-3x^2-12x+7
-1 and 2
100
Find the intervals where f(x) is increasing
f(x)=2x^3-3x^2-12x+7
(oo,-1],(2,oo)
100
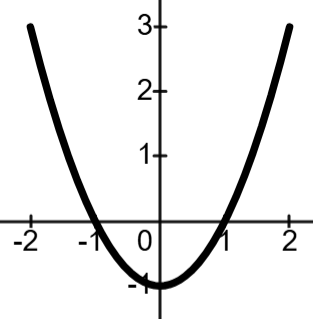Given f'(x), find the x-value of any relative maximums
-1
100
f(x)=sec(2x)
f'(x)=
2sec(2x) tan(2x)
200
lim_(x->0)(5x^2+3x^5)/(2x^3-x^2)
-5
200
If x^2+y^2+xy=3
Find dy/dx at (1, 1)
-1
200
Find the critical values on [0,2pi)
f(x)=sin^2x
0, pi/2, pi, (3pi)/2
200
Find the x-value of any points of inflection
f(x)=2x^3-3x^2-12x+7
1/2
200
Given f'(x), how many critical points does f(x) have?
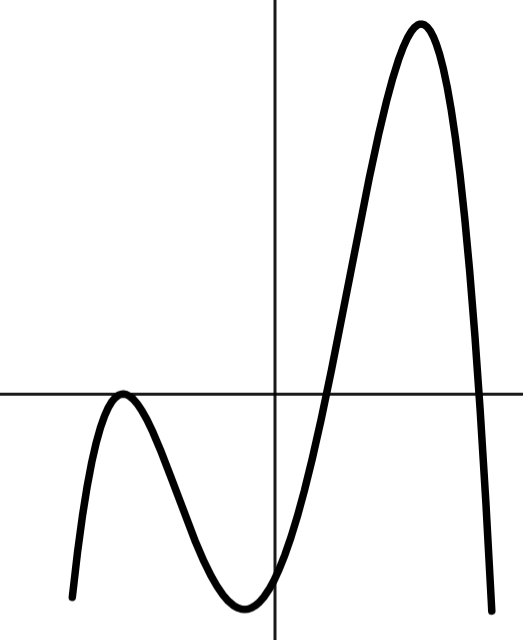
3
200
f(x)=2xcotx
f'(x)=
2cotx-2xcsc^2x
300
lim_(x->oo)((2x-3)(4-x))/((5x+1)(x+4))
-2/5
300
If x^2+2x+y^4+4y=5
then dy/dx=(-(x+1))/(2(y^3+1))
Write the equation of the tangent line that passes through the point (-2, 1)
y-1=1/4(x+2)
300
Find the critical values
f'(x)=x(2x-3)(x^2+1)
0, 3/2
300
Find all relative extrema and classify them as minimum or maximum
f'(x)=(x-2)^2(2x+3)(x^2+3)
minimum at
-3/2
300
Given g'(x), find the x-values of relative extrema for g(x)
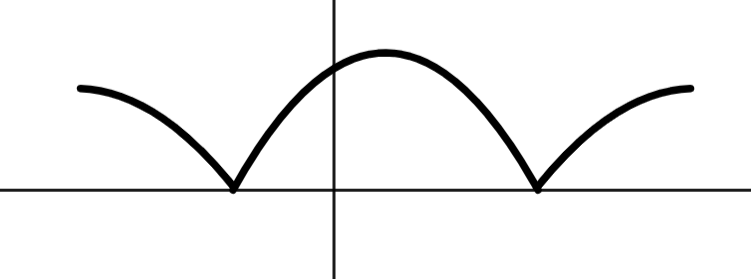
none
300
f(x)=sin^2(3x+4)
f'(x)=
6sin(3x+4)cos(3x+4)
400
lim_(h->0)(3(x+h)^2-3x^2)/h
6x
400
If x^2+2x+y^4+4y=5
then dy/dx=(-(x+1))/(2(y^3+1))
Find the two points with vertical tangents
(-4, -1) and (2, -1)
400
Find the x-value(s) of any relative minimum(s)
f(x)=2x^3-3x^2-12x+7
2
400
In right triangle ABC, where C is the right angle, leg BC is x and the hypotenuse is 5. If angle A increases at a constant rate of 3 radians per minute, at what rate is x increasing when x equals 3 units?
12
400
Given f'(x), on what interval is f(x) concave down?
x > 0
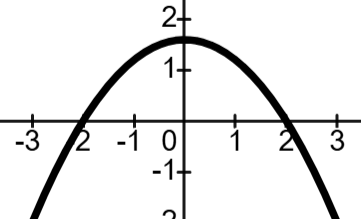
400
f(x)=sin(cos(2x))
f'(x)=
-2sin2xcos(cos2x)
500
lim_(h->0)(sin(pi/3+h)-sin(pi/3))/h
cos(pi/3)=1/2
500
If x^2+xy=-27
Find the 2 x-values where the tangent line is horizontal
sqrt27, -sqrt27
500
Find the absolute maximum on [-3, 4]
f(x)=2x^3-3x^2-12x+7
39 (when x=4)
500
Find the maximum acceleration on the interval [0, 3] by a particle with velocity v(t)=t^3-3t^2+12t+4
21 (when t=3)
500
Given f(x), which labeled x-value are f' and f'' both negative?
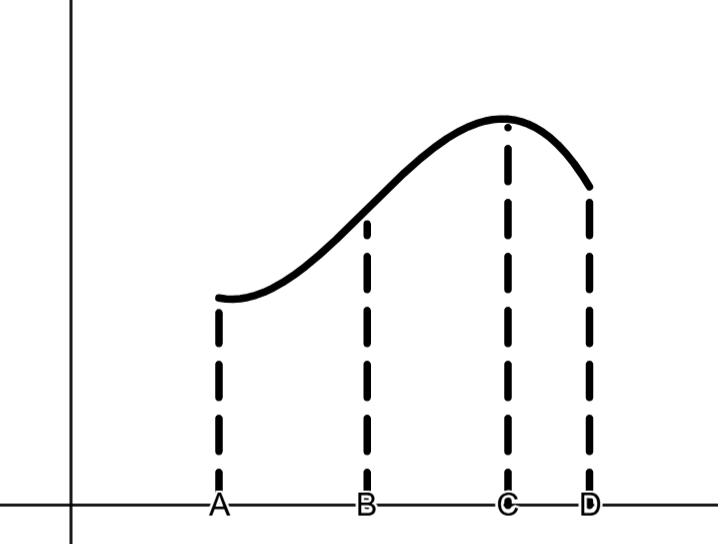
D
500
y=f(sin^2x)
y'=
2sinxcosxf'(sin^2x)