Dubious Derivatives
Intricate Integrals
Conceptual Concepts
Graph Galore
Magnificent Miscellaneous
1
The First Derivative gives you...
If the slope is increasing or decreases (can be done by point also)... Critical Values
1
∫ 8x^3 dx
2x^4 + C
1
Describe the Intermediate Value Theorem
if “f” be a continuous function over a closed interval [a, b] with its domain having values f(a) and f(b) at the endpoints of the interval, then the function takes any value between the values f(a) and f(b) at a point inside the interval
1
What is the limit at X = 2
The limit does not exist
1
Find y′ by implicit differentiation for tan(x^2 y^4)=3x+y^2
y′=3−2xy^4sec^2(x^2 y^4)4x^2y^3sec^2(x^2 y^4)−2y
2
y = 5x - 4
y' = 5
2
What does taking the integral do?
Find the total distance at any instance of time (AKA the area under the graph)
2
What is the second fundamental theorem of calculus?
2
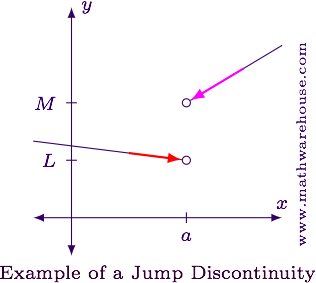
What is the negative limit of x=a?
L
2
Find two positive numbers whose sum is 300 and whose product is a maximum
x=150 y=150
3
The Second Derivative gives you...
The Concavity of a line on a graph
3
The derivative of the (indefinite) integral of the function f(x) is
f(x)
3
What is the first fundamental theorem of calculus?
Let f be a continuous function on the closed interval [a, b] and let A (x) be the area function. Then A′(x) = f (x), for all x ∈ [a, b]
3
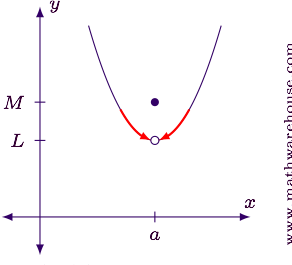
What type of discontinuity is this?
Removable discontinuity
3
Two people are at an elevator. At the same time one person starts to walk away from the elevator at a rate of 2 ft/sec and the other person starts going up in the elevator at a rate of 7 ft/sec. What rate is the distance between the two people changing 15 seconds later? (Think triangle)
7.2801 ft/sec
4
Take the second derivative of:
y = x/(x + 5); x ≠ -5
-10/(x+5)^3
4
∫(x^e+e^x+e^e) dx
x^(e+1)/e+1 + e^x + e^e x + C
4
What is the Mean Value Theorem?
if a function f is continuous on the closed interval [a,b] and differentiable on the open interval (a,b), then there exists a point c in the interval (a,b) such that f'(c) is equal to the function's average rate of change over [a,b]
4
What is the positive limit of x=-1?
-2
4
We want to build a box whose base length is 6 times the base width and the box will enclose 20 in^3. The cost of the material of the sides is $3/in^2 and the cost of the top and bottom is $15/in^2. Determine the dimensions of the box that will minimize the cost.
w=0.7299 l=4.3794 h=6.2568
5
Take the second derivative of:
y = sin^3(x)
y'' = 9sin^3(x) - 6sin(x)
5
Integrate 1/(1+x^2) for limit [0,1]
pi/4
5
What is the Extreme Value Theorem?
if a function is continuous on a closed interval [a,b], then the function must have a maximum and a minimum on the interval
5
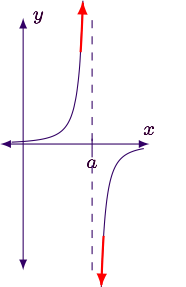
Is is this graph continuous and differentiable at every point? if not, list at what x-value both of these occur.
NO, x=a
5
The angle of elevation is the angle formed by a horizontal line and a line joining the observer’s eye to an object above the horizontal line. A person is 500 feet way from the launch point of a hot air balloon. The hot air balloon is starting to come back down at a rate of 15 ft/sec. At what rate is the angle of elevation, θθ, changing when the hot air balloon is 200 feet above the ground.
−0.02586 degrees per sec