lim_(x->4^-)((x-4))/abs(x-4)
-1
If y is the function defined below. Find dy/dx
y=3x^4sec(2x)
12x^3sec(2x)+3x^4sec(2x)tan(2x)2
lim_(x->0)((e^(2x)-sinx)/(x^2+2x))
1/2
A particle is moving along the x-axis for t greater than 0. The position of the particle is given below. At what time,t, does the particle change directions?
x(t)=t^3-9t^2-21t+6
t=7
Find f'(x)
f(x)=sqrt(4-x^2)
1/2(4-x^2)^(-1/2)(-2x)
Find the value of c that makes h(x) continuous at x=3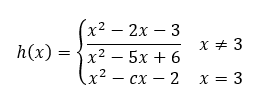
c=1
Find
f'(2) if f(x)=7x-3+lnx
7.5
Given the equation below find the state derivative
x^2+y^2=25
(d^2y)/(dx^2)
(-y+x(-x/y))/y^2
What is the acceleration of the particle at the point where the velocity is first equal to 0? If the position of a particle is given by:
x(t)=sint-cost
-sqrt(2)
f(x)=sqrt(25-x^2)
Write an equation to the tangent line to the graph of f(x) at x=-3
y-4=3/4(x+3)
lim_(x->-5)(x^2+4x-5)/(x^2+3x-10)
6/7
Find y'
y=(x^3-cosx)^5
5(x^3-cosx)^4(3x^2+sinx)
Given the following information, find
(f^(-1))'(5)
f(10)=5 and f'(10)=8
1/8
The position of a particle moving along a line is given below. Is the particle speeding up or slowing down at t=2
s(t)=t^3-12t^2+21t+10
speeding up

A
lim_(x->1)(e^(1-x)-x)/(x^2-1)
-1
Find y''
y=x^2f(x)
2f(x)+4xf'(x)+x^2f''(x)
Find f''(x)
When
f(x)=(1+x/20)^5
1/20 (1+x/20)^3
CALCULATOR
If v(t) is representing by the function below is this particle speeding up or slowing down when t=1. EXPLAIN your answer.
v(t)=sin(t^1.5)
Speeding up a(1) and v(1) are the same sign.
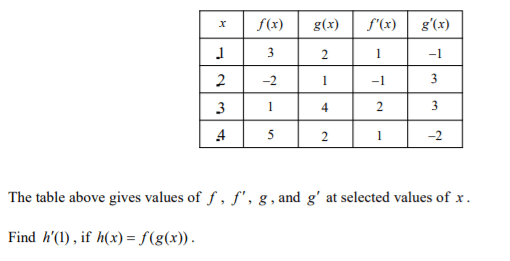
1
lim_(h->0) (sin(x+h)-sin(x))/h
cos(x)
Find y' if
y=3cos^2(4-x)
y'=3cos(4-x)(-sin(4-x))(-1)
Find the equation of the tangent line to the graph f(x) at the point (1,-3)
y+3=11/3(x-1)
A particle movies along the x-axis with its position at time t given by x(t) below, where a and b are constants and a does NOT equal b. Find the value of t where the particle is at rest.
x(t)=(t-a)(t-b)
t=(a+b)/2
Let f(x) be continuous and contain the points (0,1) and (2,1) name a point that would make f(x)=0 at least twice in the interval 0<x<2
BONUS 100: If you can state this topic that proves your answer.
various answers
Example (1,-1)
IVT