Segment Bisectors
Midpoint and Distance Formula
Perimeter and Area
Identifying Angles
Angle Postulates and Theorems
100
1) Identify the Segment Bisector of Segment RS.
2) Find RS and MS.
1) Segment Bisector is Line s
2) MS = 15 and RS = 30
100
Given a segment AB on the coordinate plane with endpoints A(2, 4) and B(12, 14). Find the coordinates of the midpoint M.
Midpoint: M(7, 9)
100
Classify the polygon by the number of sides and tell whether it is convex or concave.
3. Concave Quadrilateral
4. Convex Triangle
5. Convex Pentagon
6. Concave Hexagon
100
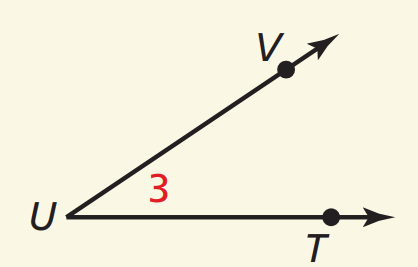
Write four names for the Angle below:
100
1) Write the Angle Addition Postulate statement for the diagram below.
2) Find m<ABC.
1. m<ABD + m<DBC = m<ABC
2. m<ABC = 103 degrees
200
1) Identify the segment bisector of Segment RS.
2) Find RM and MS.
1) Segment Bisector is Ray MA. 
2) RM = 13 and MS = 13
200
Given a segment AB on the coordinate plane with endpoints A(3, -5) and B(7, 9). Find the coordinates of the midpoint M.
Midpoint: M(5, 2)
200
Find the Area and Perimeter of this figure in the coordinate plane.
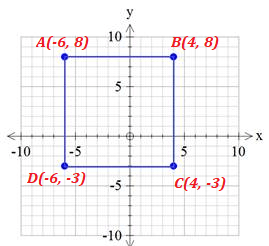
Area = l x w = 10 X 11 = 110
Perimeter = l + l + w + w = 10 + 10 + 11 + 11 = 42
200
Identify 3 pairs of congruent angles in the diagram below:
1. <C = <F
2. <A = <D
3. <B = <E
200
Find the m<CBD and m<CBA given that <CBA is being bisected by the Ray BD.
m<CBD = 65
m<CBA = 130
300
1) Identify the segment bisector of Segment JK.
2) Find the value of x and JM.
1) Point M
2) x = 22 and JM = 138
300
Find the distance between the two points: A(13, 2) and B(7, 10)
Distance = 10
300
Find the area of the triangle below:
Area = bh/2 = (12 x 10)/2 = 60
300
Find the measure of each angle and then classify each angle.
a. <RQU = 125 (obtuse)
b. <TQU = 35 (acute)
c. <UQS = 90 (right)
300
DAILY DOUBLE!!!!!!! WORTH 600 POINTS
Find the measure of each angle in the diagram:
1. m<ABD , 2. m<DBC, 3. m<ABC
x = 25
m<ABD = 135
m<DBC = 45
m<ABC = 180
400
1) Identify the segment bisector of Segment JK.
2) Find the value of k and MK.
1) Line l
2) k = 2 and MK = 39
400
Given a segment AB on the coordinate plane with endpoints A(-8, -6) and B(-4, 10). Find the coordinates of the midpoint M.
Midpoint: M(-6, 2)
400
Find the perimeter of the figure below:
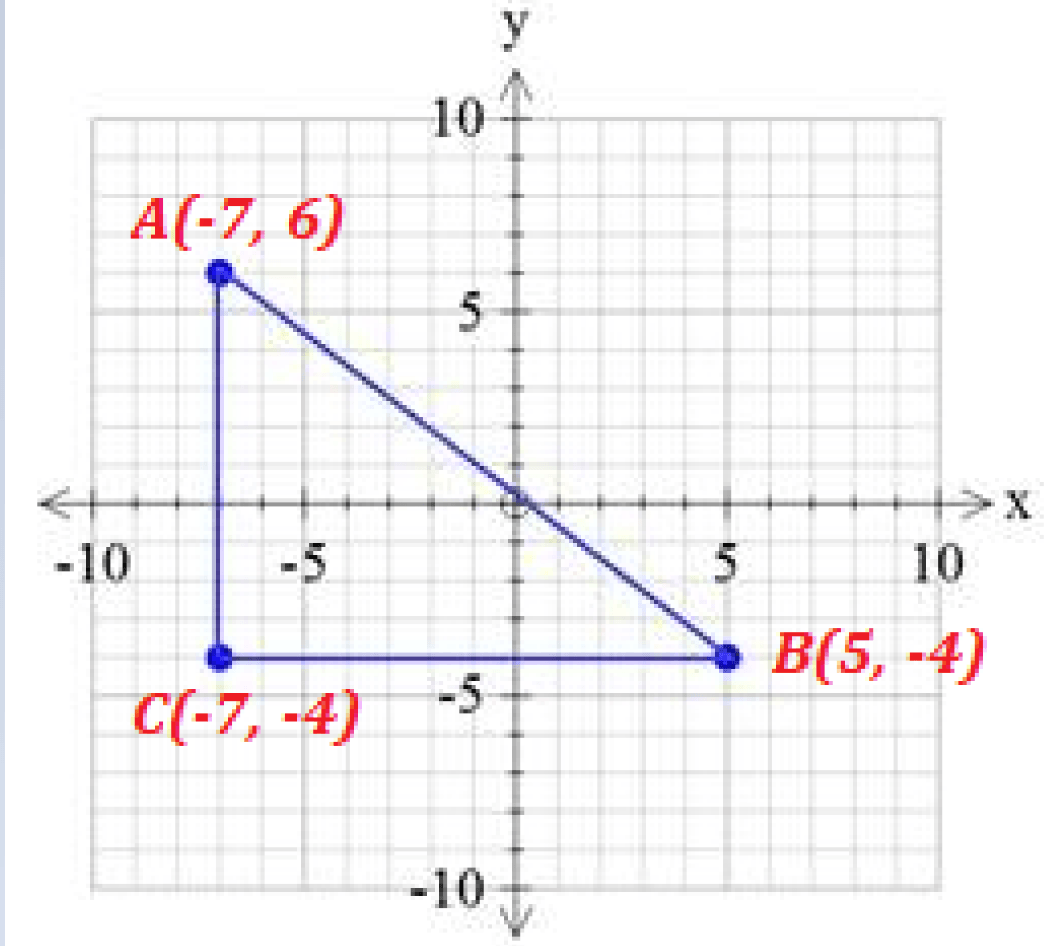
Perimeter = AC + CB + AB = 10 + 12 + 15.6 = 37.6
AB = sqrt((5--7)^2+(-4-6)^2)
AB = sqrt((12)^2+(-10)^2)
AB = sqrt(144+100)
AB = sqrt(244)
AB = 15.6
400
If m<A = 25 degrees and m<E = 97 degrees, find m<B and m<D.
m<D = 25 degrees
m<B = 97 degrees
400
Given that m<ABC = 143, find m<ABD and m<DBC.
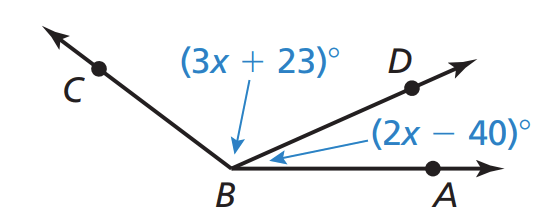
m<ABD = 24
m<DBC = 119
x = 32
500
1) Identify the segment bisector of Segment XY.
2) Find the value of x and XY.
1) Ray MN 
2) x = 5 and XY = 32
500
Find the distance between two points: J(-8, 0) and K(1, 4)
D=sqrt(97)=9.8
500
Find the area and the perimeter of the figure below:
Area = bh/2 = (4 x 3)/2 = 6
Perimeter = AB +BC + AC = 3.6 + 3.6 + 4 = 11.2
AB = sqrt((0-2)^2+(1-4)^2)
AB = 3.6
BC = sqrt((2-4)^2+(4-1)^2)
BC = 3.6
500
Which angle name does not belong with the other three? Explain your reasoning.
<BCA does not belong because, the other three names refer to the same angle.
500
Ray BD bisects <ABC. Find m<ABD, m<CBD, and m<ABC.
m<ABD = 67
m<DBC = 67
m<ABC = 134