Is this a function? 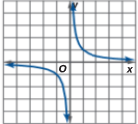
Yes, it is. It passes the vertical line test.
Is
f(x) = x^2-3x
continuous at x=4?
Yes.
State the domain and range of the following graph:
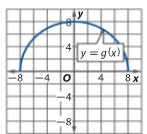
D: [-8,8]
R: [0,8]
f(x) = 3x + 6, g(x) = 2x - 5
Find (f+g)(x)
(f+g)(x) = 5x+1
Given f(x) = 2x+ 1 and g(x) = 3x2
What is (f o g)(x)?
(f o g)(x) = 6x2 + 1
Determine if 3x-2y = 18 represents y as a function of x.
y =3/2x - 9
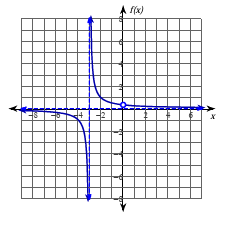
Describe the following graphs end behavior:
lim_(x->-oo)=2, lim_(x->oo)=2
Use the graph to determine the domain and range for the function.

D: All Reals
R: All Integers
f(x) = x^2 + 6, g(x) = 2x^4 + 5x - 4
Find (f-g)(x)
-2x^4 +x^2-5x+10
Given f(x) = 2x+ 1 and g(x) = 3x2
What is (g o f)(x)?
12x^2+12x+3
Does 4y2 + 18 = 96x represent y as a function of x?
No, it is not a function
y = sqrt(24x-9/2
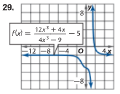
Determine if
f(x) = x/(x^2 + 3x); x=-3 and x=0
is continuous at the given x-values and if not continuous classify the type of discontinuity
x = - 3 is an infinite discontinuity
x = 0 is a removable discontinuity (or a hole)
Identify the parent function of
f(x) = 1/6x +7
Describe the transformations from the parent function to f(x)
f(x) = x
Translation up 7
Slope flatten by a factor of 6
f(x) = x+3, g(x) = x - 6
what is
(f*g)(x)
(f*g)(x) = x^2-3x-18
Given
f(x) = sqrt(x-4), g(x) = x^2 + 1
What is (g o f)(x) and what is the domain?
x - 3
Domain : [4,infinity]
Does
f(x) = 3 + sqrt(x^2 - 4)
represent f(x) as a function of x? Evaluate f(3x).
Yes, it is a function.
3+ sqrt(9x^2 - 4
Determine if
f(x) = x^2/(x+1); x = -1
is continuous at the given x-values and if not continuous, classify the type of discontinuity
Infinite discontinuity at x = -1
Use the graph of the function find it's y-intercept and zero(s). Verify using algebra.
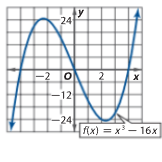
zeros at -4, 0, and 4.
f(x) = 3x3 - 4x + 5, g(x) = 2x2 - 2
what is
(f*g)(x)
6x^5-14x^3+10x^2+8x-10
Given
f(x) = sqrt(x-4), g(x) = x^2 + 1
What is (f o g)(x) and what is the domain?
(fog)(x) = sqrt(x^2-3)
Domain:
(-oo,-sqrt(3)]uu[sqrt(3),oo)
Is
g(x) = sqrt(6x - 3)
a function? State the domain of the relation in set-builder notation.
Yes, it is a function
{x | x >= 0.5 , x in RR}
Determine if
f(x) = x/(x^2-4x)
is continuous and if not continuous, find the discontinuities and classify them.
Removable discontinuity at x=0
Infinite discontinuity at x = 4
Graph this function
f(x) = {(-x^2, if x < -2), (3, if -2 <= x < 7), ((x-5)^2 + 2, if x >= 7):}
Rapidly increasing to -2, constant between -2 and 7, rapidly increasing from 7 to infinity.
f(x) = 3/x, g(x) = x^4
Find (f/g)(x). State the domain.
(f/g)(x) = 3/x^5
Domain is All Reals but x is cannot be equal to 0.
Given
f(x) = 4/(x+2), g(x) = 1/x
Find (f o g)(x) and the domain.
(f o g)(x) = (4x)/(1+2x), x !=0,x!=-1/2,x!=-2