Properties of Equality
Solving Equations
Relations
Functions
Interpreting Graphs of Functions
100
Write an algebraic expresssion to represent the number of pens that can be bought with 30 cents if each pen costs c cents.
30c
100
Solve r=(7(16-5))/(3+4(2))
7
100
Find the domain and range of this relation.
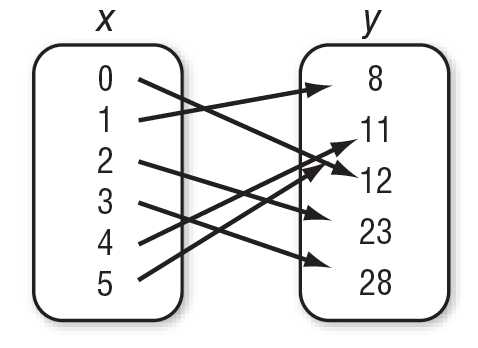
Domain: {0,1,2,3,4,5}
Range: {8, 11, 12, 23, 28}
100
True or False: Relation is always a function
False
100
What is x and y intercepts?
x-intercept is where the graph crosses the x-axis and y-intercept is where the graph crosses the y-axis.
200
Evaluate (7a+b)/(b+c) if a=2 , b=6, and c=4 ?
2
200
Find the solution set of 3a+12=39 if the replacement set is {6,7,8,9,10} .
{9}
200
What is the domain of this relation?
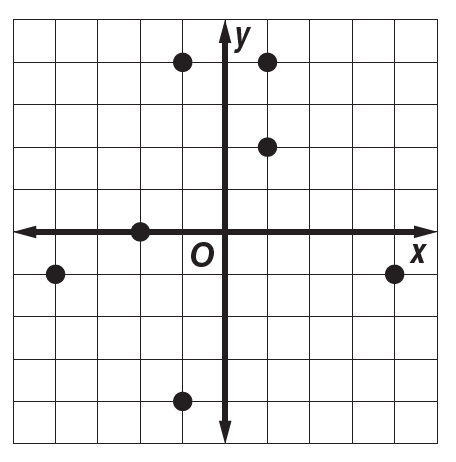
{-4,-2,-1,1,4}
200
Is the given relation a function or not?
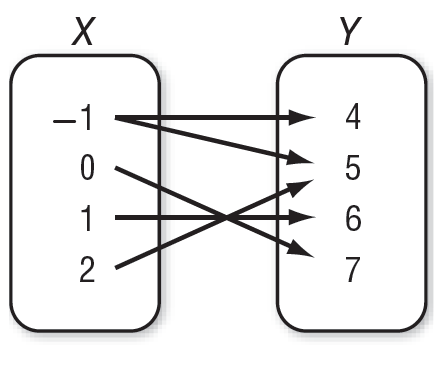
Not a Function
200
What is x and y intercepts?
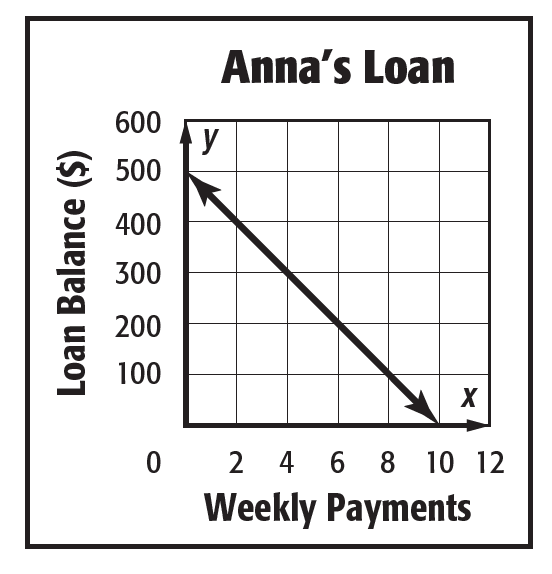
x=10 and y=500
300
Evaluate 2[1/4+(1/2)^2]
1
300
Candice is typing an average of 40 words per minute. Find the time it will take her to type 1000 words.
25 minutes
300
Identify the Independent and Dependent variable: How long you sleep affects your test score.
Independent: Number of hours of sleep
Dependent: Test score
300
If f(x)=2x^2-4 , what is f(-2) ?
4
300
What is y-intercept?
y=30
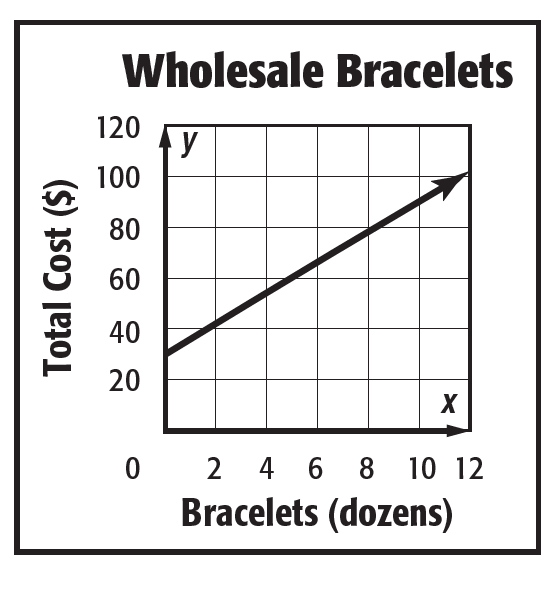
400
Simplify 4(6p+2q-2p)
24p+8q-8p
400
Solve
28/b+9=16
4
400
What is the independent and dependent variable?
Independent: Time
Dependent: Price
400
Is this a function?
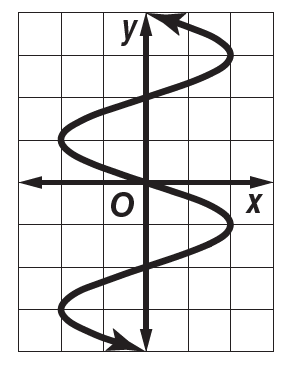
No
400
Interpret the end behavior
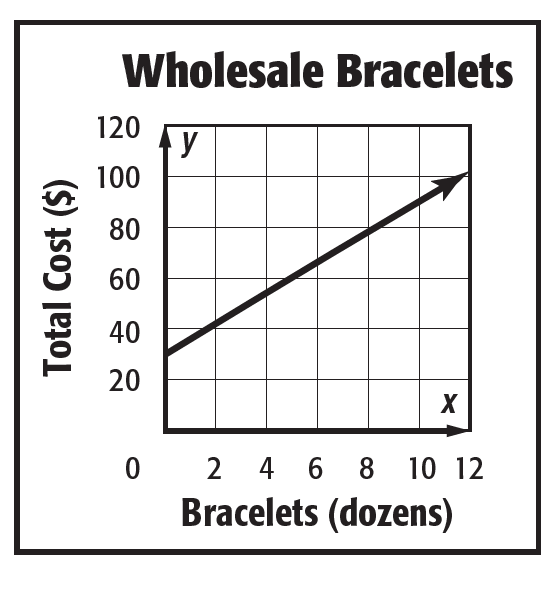
As x increases, y also increases whereas the total cost increases.
500
Evaluate (5^2*4-5*4^2)/(5(4)
1
500
Gabriel pays $40 a month for basic cell phone service. In addition, Gabriel can send text messages for $0.20 each. Find the total amount Gabriel spent this month if he sends 40 text messages.
$48
500
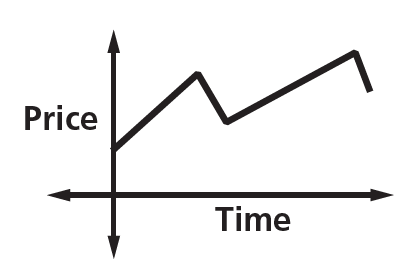
Describe what is happening on the graph.
The price increases steadily, then it falls, then increases, then falls again.
500
If f(x)=2x^2-6 , find f(h+2) .
2h^2+8h+2
500
What is intercept/s and end behavior?
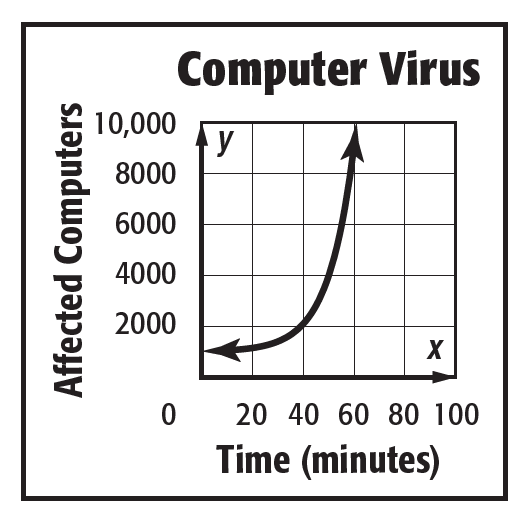
(y=1000)1000 computers were affected when time started.
As x increases, y also increases whereas the number of affected computers is expected to continue to increase.