Fill In the Blank
Completing Identities
Proving Identities
Finding Exact Values
Review of All
100
When proving an identity, it is a good idea to start with ________?
The most complicated side
100
tan2(theta)=
sin2(theta)/cos2(theta)
100
What side should you start with first?
cosx+tanxsinx= secx
Left
100
What is the difference formula for cos and sin?
(2 answers)
100
Find the cosine of 112.5 degrees using a half angle formula.
- 
200
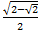
An equation is an identity when it is true for ____ of the possible values of the variable in the domain.
all
200
2/cos(theta)=
2sec(theta)
200
Which side should you start with first?
cot2x= cosx/sinxtanx
Right
200
What is the identity for sin(a+b)?
200
If cosx=(8/17) in Q4, find tan(x/2)
(-3/5)
300
When proving an identity, make sure to change all of the terms to ___ or ___.
sine, cosine
300
1/cos2(theta)=
sec2(theta)
300
What would be your very first step when proving this identity?
(sinx+cosx)2=1+2sinxcosx
The first thing you would do is foil the (sinx+cosx)2
300
Use the sum formula to find the exact value of cos165(degrees)
Use 135+30
-sqrt6-sqrt2/4
300
Use the half of double angle formula to find cos660(degrees)
(1/2)
400
There are ___ Pythagorean identities.
Three
400
csc2(theta)=
1/sin2(theta)
400
What would be the first two steps when trying to prove this identity?
tan2x+1=sec2x
1. change the left side to sin2x/cos2x + 1
2. add cos2x/cos2x (replaces the +1)
400
Use the sum formula to find the exact value of tan75(degrees)
Use 45+30
3+sqrt3/ 3-sqrt3
400
If tanx=(-5/12) in Q2, find the exact value of cos2x.
(119/169)
500
All identities are ______, but not all ______ are _____.
equations, equations, identities
500
sin2x+cos2x=1 can also be written as...
cos2x=1-sin2x / sin2x= 1-cos2x
500
Prove that secxtanx(1-sin2x)= sinx
I will come check your work
...
500
Find the sine of 75 degrees using a half angle formula.
500
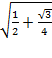
What would be the correct sum formula if you had to solve with tan?
tan (A + B) = 