Volume
Pythagorean Theorem
Find Missing Angles
Interior/Exterior Angles of Triangles
Exponents
100
What is the volume of a rectangular prism with length 4 cm, width 3 cm, and height 5 cm?
60cm3
100
What is the length of the hypotenuse of a right triangle with legs 3 and 4 units long?
5 units
100
What is the relationship shown? Solve for ?
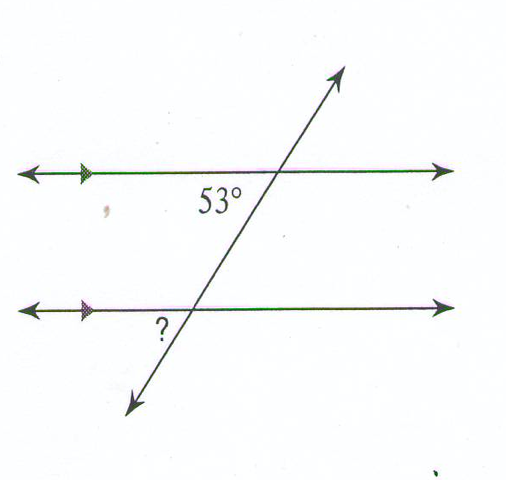
Corresponding
53 degrees
100
What is the sum of the interior angles of a triangle?
180 degrees
100
Simplify: 50
1
200
Find the volume of a cylinder with a radius of 3 cm and a height of 10 cm.
282.74cm3
200
A right triangle has one leg of 6in and a hypotenuse of 8in. What is the other leg?
5.3in
200
Name the relationship and solve for x
Vertical Angles
x=10
200
Solve for each angle
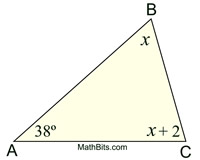
A= 38 degrees
B= 70 degrees
C= 72 degrees
200
Simplify: (23) x (24)
27
300
340.34cm3
300
Use the Pythagorean Theorem to find the distance between the points (-2,1) and (4,3). Round to the nearest tenth.
6.3 units
300
Solve for x and y. Name the relationship
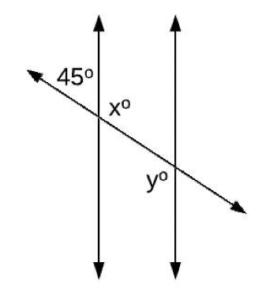
Alternate Interior
X=135 Y=135
300
Solve for z and the exterior angle
z=111
Exterior angle= 141 degrees
300
Simplify: (3x2)3
27x6
400
904.78in3
400
A hiker begins at a ranger station and hikes 5.6 miles directly south to a river. Then, she hikes 9.3 miles directly east along the river to reach a campsite. She later returns to the ranger station by hiking in a straight line through the forest.
How far is the ranger station from the campsite, to the nearest tenth of a mile?
approximately 10.9 miles
400
Two parallel lines are cut by a transversal. One angle measures 4x+10, and its same-side interior angle measures 6x−20. Find the value of x and both angle measures.
x=19
angle 1 = 86 degrees
angle 2 = 94 degrees
400
In a triangle, two interior angles are each 3x and the third is 2x. Find the value of x and each angle.
x=22.5
Angles: 45 degrees, 67.5 degrees, 67.5 degrees
400
Rewrite with no negative exponents: x-3y2
y2/x3
500
A cylindrical tank has a radius of 4m and a height of 6m. 1/4 of the tank is filled with water. How many more cubic meters of water would need to be added to fill the tank?
226.08m3
500
ABCD is an isosceles trapezoid.
What is the length of AD?
17cm
500
Name the relationship and find the missing angles
linear pair
x= 41 degrees
y= 90 degrees
z= 41 degrees
500
In triangle ABC, one exterior angle at vertex A measures 120 degrees. The two remote interior angles are in a ratio of 2:3. What are the measures of the two remote interior angles?
48 degrees
72 degrees
500
Simplify the expression: (4x-2y3)/(2x-5y)
2x3y2