Operations with Rational Functions
Simplifying & Solving Radicals
Graphing Rational Functions & Piecewise Functions
Writing Functions
Polynomial Operations & End Behavior
100
Multiply
(x^2+3x)/(x^2+6x+8)*(x^2+x-2)/(4x^3+12x^2)
(x-1)/(4x(x+4)
100
Simplify.
5root(3)(54a^5b^9)
15ab^3root(3)(2a^2)
100
Find the vertical asymptote(s).
f(x)=(x+2)/((x+3)(x-2))
x=-3, x=4
100
Write the piecewise function from the given graph.
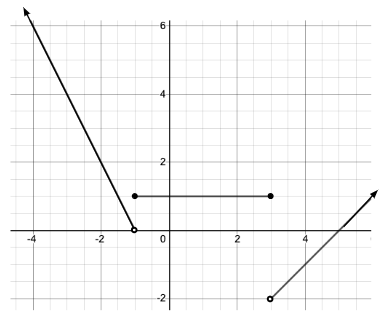
{(-2x -2, if x<-1), (1, if -1<=x<=3), (x-5, if x>3):}
100
Multiply.
(4x^3+2x-5)(x^2+3)
4x^5+14x^3-5x^2+6x-15
200
Divide.
(x-3)/(x^2-5x-14)-:(x^2-x-6)/(x-7)
1/(x+2)^2
200
Multiply and simplify.
root(4)(8xy^3)*root(4)(2xy)
2ysqrt(x)
200
Identify the zeros, vertical, and horizontal asymptotes.
f(x)=(x^2+3x+2)/(x-3)
zeros:
(-2,0) & (-1,0)
vertical asymptote:
x=3
horizontal asymptote: none
200
Find the inverse of
f(x)=3/4x+6
f^-1(x)=4/3x-8
200
Multiply.
(2x-3)^4
16x^4-96x^3+216x^2-216x+81
300
Add
3/(x^2-9)+2/(x+3)
(2x-3)/((x+3)(x-3))
300
Write in radical form.
x^(3/4)
root(4)(x^3)
300
Find
f(4)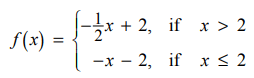
f(4)=17
300
Find the inverse of
f(x)=3sqrt(x+2)
f^-1(x)=x^2/9-2
300
Divide.
(5x^2-6x-8) -: (x-2)
5x+4
400
Subtract
6/(x^2+2x+1)-1/(x+1)
(-x+5)/(x+1)^2
400
Simplify.
root(3)(8/(3x^2))
(2root(3)(9x))/(3x)
400
Graph the piecewise function.
400
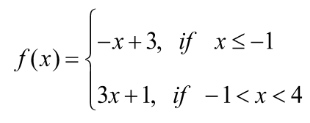
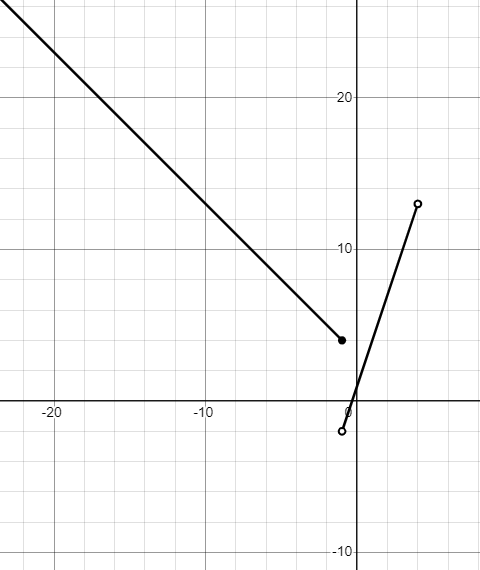
Find
f(g(x))
if f(x)=x^2+6x+2 and g(x)=x+1
f(g(x))=x^2+8x+9
400
Given the function, identify the parent function and the transformations.
y=1/5sqrt(x+4)-1
parent function: square root
-vertical compression of 1/5
-left 4
-down 1
500
Solve for x.
(x+1)/(x-3)=3/x+12/(x^2-3x)
x=3, -1
500
Solve.
sqrt(8w+1)=w+2
w=3,1
500
Find the hole(s), horizontal asymptote(s), vertical asymptote(s), x-intercept(s), and y-intercept. Then graph.
(x^2-5x+6)/(x^2+2x-15)
hole:
at x=3
horizontal asymptote:
y=1
vertical asymptote:
x=-5
x-intercept:
(2,0)
y-intercept:
(0, -2/5)
500
Write an exponential function that models this data. Then find when the number of bacteria reaches 2500.
y=349.98(1.18)^x
about 11.88 min
500
Compare the end behavior of the functions.
f(x)=1/2x^3 and g(x)=-1/2x
as x-> - oo, f(x)-> -oo
as x-> oo, f(x)-> oo
as x-> - oo, g(x)-> oo
as x-> oo, g(x)-> -oo