Linearization
Relative Rates of gRowth
f(x) & f'(x)
Extrema
Related Rates (2x pts)
100
Find the tangent line to the curve
f(x)=cos^2(x)
when x=0
f'(x)=-2cos(x)sin(x)
f'(0)=0
f(0)=1
y=1
100
Which grows faster (show proof):
f(x)=x or g(x)=3x^3
3x^3
100
Find the intervals of increase and decrease for the function
h(x)=x^2/2+x+5/2
Increases:
(-1,infty)
Decreases:
(-infty,-1)
100
Find the relative extrema for the function
g(x)=x^2-2x+3
Min:
(1, 2)
100
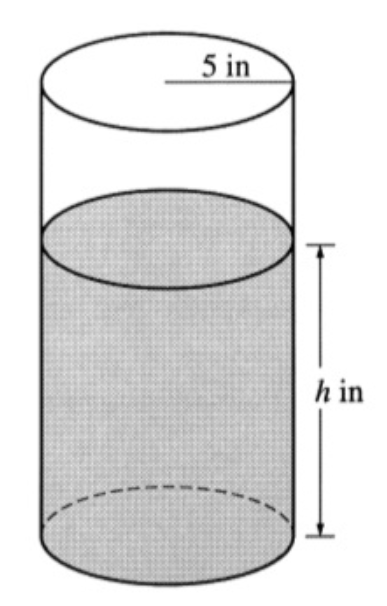Find the volume of water in the cylinder
25pih
200
Find the tangent line to the curve
x^2e^x
when x=1
f'(x)=e^x(x^2+2x)
f'(x)=3e
f'(1)=e
y-e=3e(x-1)
200
Which grows faster (show proof):
f(x)=e^x or g(x)=cos(x)
e^x
200
Find the intervals of increase and decrease for the function
h(x)=x^3-x^2+3
Increases:
(-infty, 0)and(2/3,infty)
Decreases:
(0,2/3)
200
Find the relative extrema for the function
g(x)=x^3+3/2x^2-1
Max:
(-1,-0.5)
Min:
(0,-1)
200
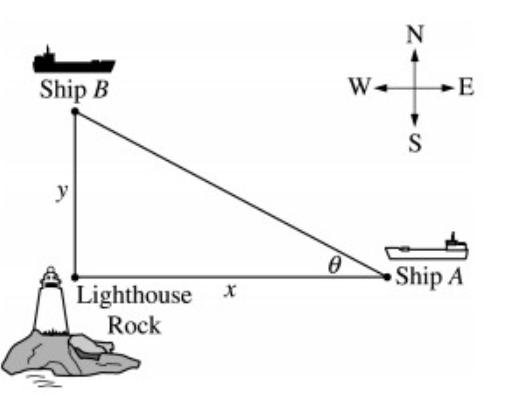Ship A is traveling due west toward Lighthouse Rock at a speed of 15 kilometers per hour (km/hr). Ship B is traveling due north away from Lighthouse rock at a speed of 10 km/hr. Let x be the distance between Ship A and Lighthouse Rock at time t, and let y be the distance between Ship B and Lighthouse Rock at time t, as shown in the figure above.
Find the distance, in kilometers, between Ship A and Ship B when x = 4 km and y = 3 km
5 km
300
Use linearization at x=3 to approximate f(3.1) of the function
f(x)=-\sqrt (x+6)
f'(x)=(-1/2)(x+6)^(-1/2)
f'(3)=-1/6
f(3)=-3
y+3=-1/6(x-3)
y=-3.0167
300
Which grows faster (show proof):
f(x)=e^-x or g(x)=ln(x)
ln(x)
300
Find the intervals of increase and decrease for the function
h(x)=-2/(x^2+2)
Increases:
(0,infty)
Decreases:
(-infty,0)
300
The function f is defined by
x^2e^(-x^2)
At what values of x does f have a relative maximum?
x=-1
and
x=1
300
Ship A is traveling due west toward Lighthouse Rock at a speed of 15 kilometers per hour (km/hr). Ship B is traveling due north away from Lighthouse rock at a speed of 10 km/hr. Let x be the distance between Ship A and Lighthouse Rock at time t, and let y be the distance between Ship B and Lighthouse Rock at time t, as shown in the figure above.
Find the rate of change, in km/hr, of the distance between the two ships when x = 4 km and y = 3 km.
-6 (km)/(hr)
400
Use linearization at
x=pi
to approximate f(3.16) of the function
sin(x)
f'(x)=cos(x)
f'(0)=-1
f(0)=0
y=-(x-pi)
y=-0.0184
400
Which grows faster (show proof):
f(x)=x^e or g(x)=e^x
e^x
400
Find the intervals of increase and decrease for the function
h(x)=x^2e^x
Increases:
(-infty, -2)and(0,infty)
Decreases:
(-2,0)
400
Where does the absolute maximum value of the function
g(x)=-cos(x)-sin(x)
occur on the interval
[-2, 4]
x=4
400
A cube with edges of length x centimeters has volume
V(x) = x^3
cubic centimeters. The volume is increasing at a constant rate of 40 cubic centimeters per minute. At the instant when x = 2, what is the rate of change of x, in centimeters per minute, with respect to time?
10/3
500
Use 2 iterations of Newton's Method to approximate
6^(1/3)
1.817 (with proof)
500
Which grows faster (show proof):
f(x)=\sqrt(x) or g(x)=ln(x^2)
sqrt(x)
500
Find the intervals of increase and decrease for the function
h(x)=cot(2x) [-pi,pi]
Increases: None
Decreases:
(-pi,\pi/2),(-pi/2,0),(0,pi/2),(pi/2,pi)
500
What is the absolute minimum for the function
g(x)=-cos(x)-sin(x)
on the interval
[0, pi/2]
-sqrt(2)
500
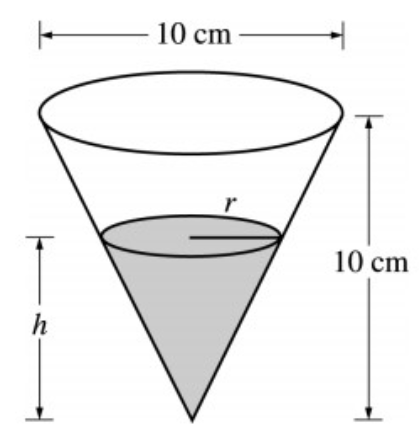
A container has the shape of an open right circular cone, as shown in the figure above. The height of the container is 10 cm and the diameter of the opening is 10 cm. Water in the container is evaporating so that its depth h is changing at the constant rate:
(dh)/(dt)=-3/10 (cm)/(hr)
V=(1/3)pi*(r^2)*h
Find the rate of change of the volume of water in the container, with respect to time, when h = 5 cm. Indicate units of measure.
-15/8 pi (cm^3)/hr