Inverse Functions
Exponential Functions
Logarithmic Functions
Miscellaneous
100
The inverse of the function:
{(1, 5), (3, 10), (2, 4)}
{(5,1), (10,3), (4,2)}
100
The inverse of the exponential function
Logarithmic Function
100
The inverse of the Logarithmic Function
Exponential Function
100
0
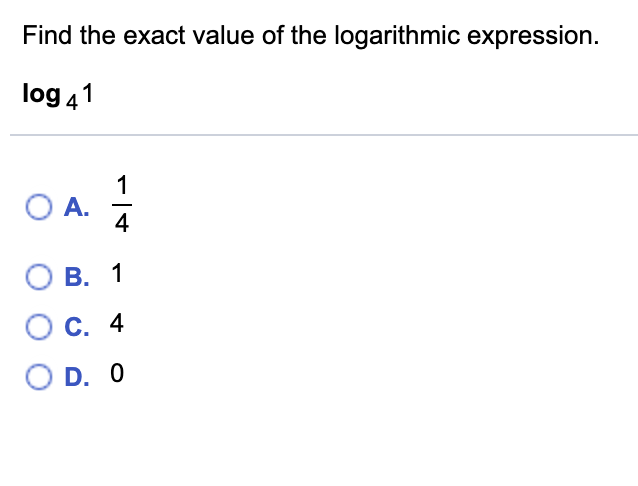
200
The inverse of the function:
{(31,1), (26,2), (21, 3), (16, 4)}
200
The domain of the exponential function 
-> The set of all real numbers
-> negative infinity to positive infinity
200
The Range of the Logarithmic Function
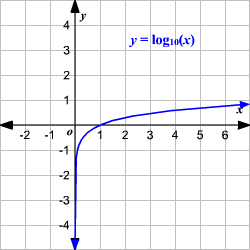
-> The set of all real numbers
-> negative infinity to positive infinity
200
The property used to write the logarithm as a single logarithm
Product rule
300
Complete the sentence: The domain of f(x) is the _________________ of its inverse. The range of f(x) is the _________________________ of its inverse.
Range and domain
300
The transformations needed to take graph the parent (red) to f(x) (blue)
Horizontal shift 2 units to the left
Vertica shift 1 unit up
300
The equivalent statement of log100=2
10 to the power of 2 equals 100
300
The domain of the function
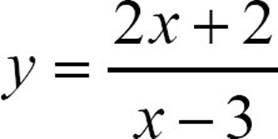
All real numbers except positive 3
400
The line that the graphs of a one-to-one function and its inverse are symmetric about 
y=x
400
The inverse of f(x)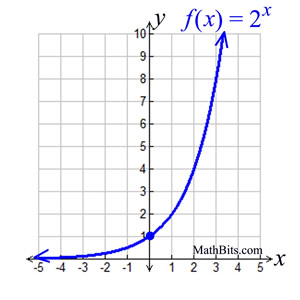
The logarithm to the base 2 of x
400
The exact values of the logarithmic expressions
4 and -3
400
The algebraic process used to show that two functions are inverses.
Composition of functions
500
The inverse of f(x)= 2x+3
What is (x-3) divided by 2
500
The value of x
x = -2
500
The Transformations that will take the red graph to the navy graph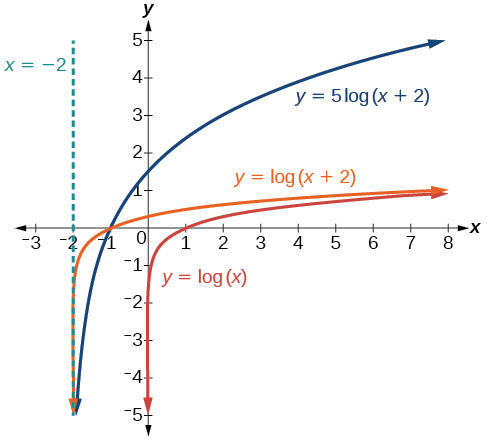
Horizontal shift left 2 and vertical stretch by a factor of 5
500
The two functions used to find the domain of a composite function
g(x) and f(g(x))