Definitions
Permutation
Combination
Tree Diagrams
100
Probability
Likelihood of something happening
100
6 P 4
360
100
5 C 4
5
100
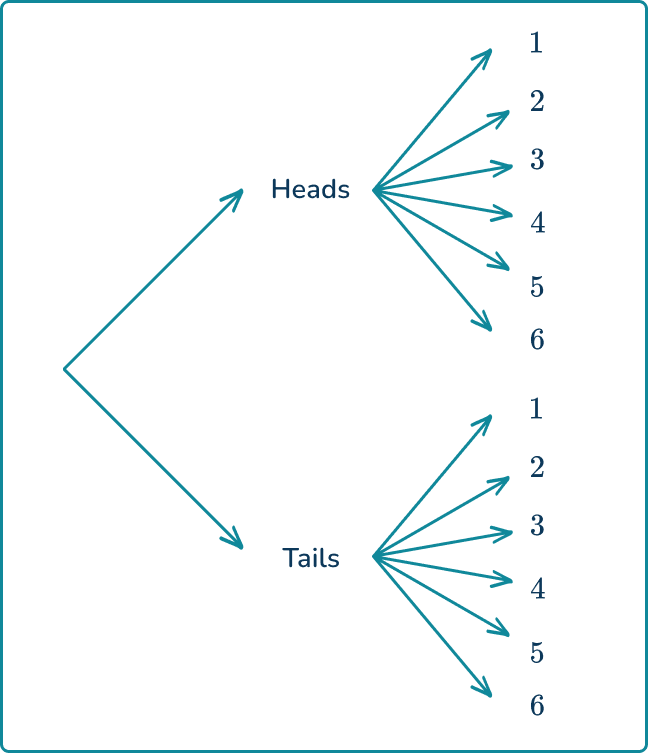How many possible outcomes?
12 outcomes
200
Sample Space
Set of possible outcomes of a random experiment or event
200
12 P 4
11, 880
200
15 C 4
32, 760
200
What is the probability of selecting a blue on the first try and red on the second try?
4/12 x 2/11
8/132
2/33
300
Permutation
Permutations are ordered arrangements where the order of selection matters
300
A group of 25 people are going to run a race. The top 8 finishers advance to the finals.
43,609,104,000
300
Double the result of 10 C 5
504
300
What is the probability of selecting the same color?
P(Red then Red) x P (Blue then Blue)
(2/12 x 1/11) + (4/12 x 3/11)
2/132 + 12/132
14/132
7/66
400
Combination
combinations are groups where the order does not matter
400
An arrangement in the word great
5x4x3x2x1 =
120
No repeated letter, so use the counting principle based on the number of letters in the word
400
How many different committees of 3 people can be chosen to work on a special project from a group of 9 people?
84
400
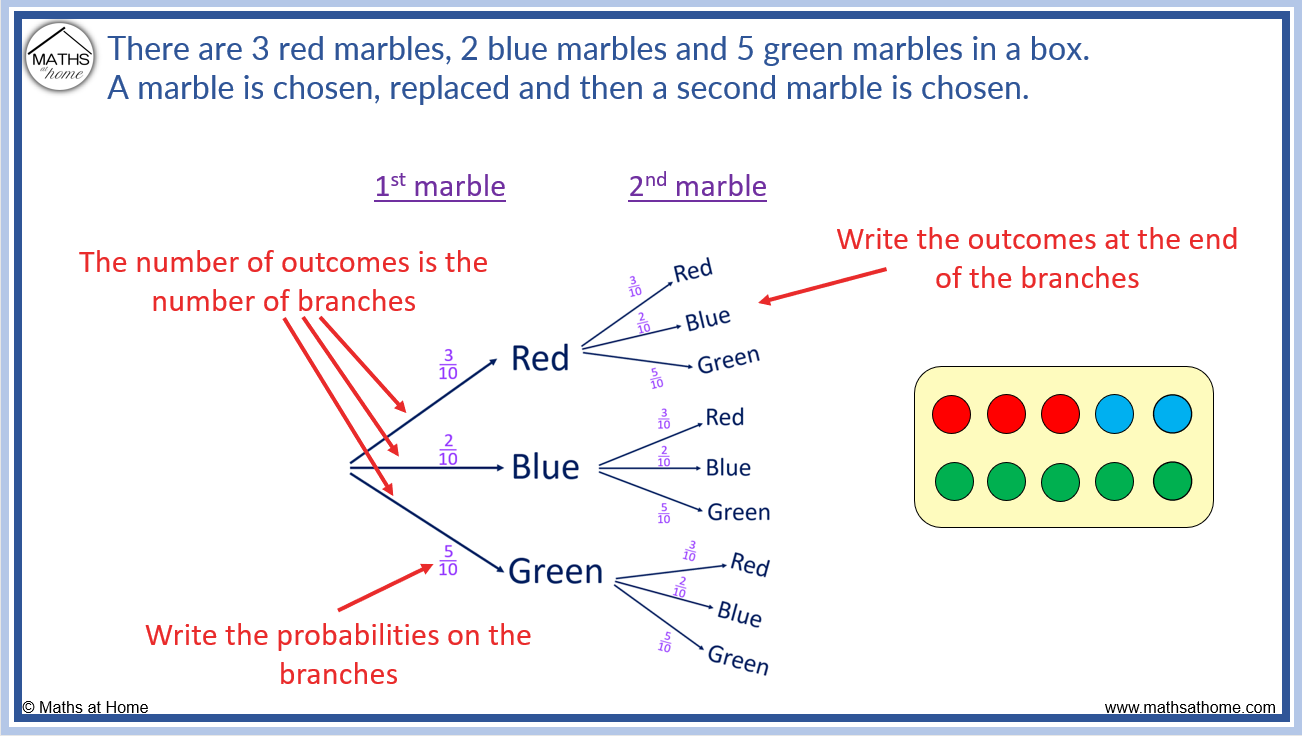
There are 3 red marbles, 2 blue marbles, and 5 green marbles in a box. A marble is chosen, replaced, and a second marble is chosen. Draw a tree diagram to represent this information. Ensure that you include the probabilities.
500
Probability Tree Diagrams
is a diagram that is used to give a visual representation of the probabilities as well as the outcomes of an event
500
An arrangement of letters in the word isosceles
9!/3!2! =
30, 240
9! - number of letters in the word
3! - number of repeated 's'
2! - number of repeated 'e'
500
From a group of 10 men and 12 women, how many committees of 5 men and 6 women can be formed
10 C 5 . 12 C 6 = 252 . 924
232, 848
500
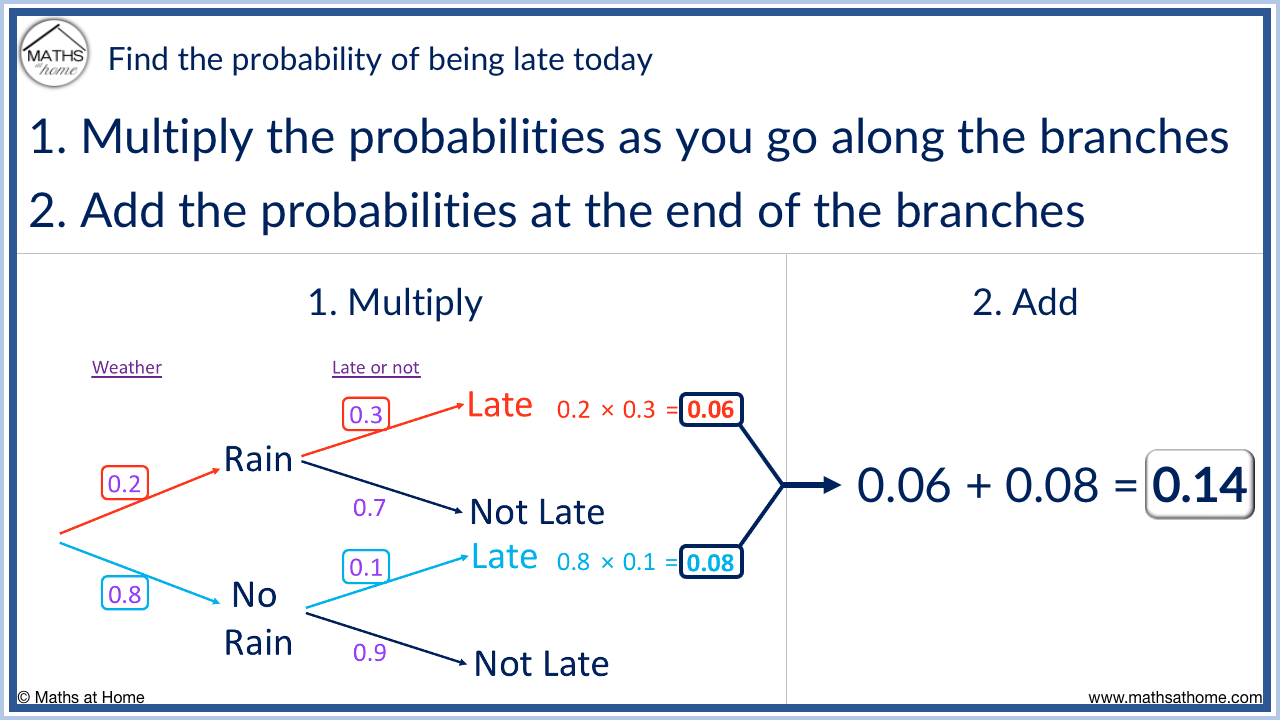
The probability of it raining is 0.2. If it rains, the probability I am late is 0.3, and if it doesn’t rain, the probability of me being late is 0.1.
a) Draw a tree diagram
b) What is the probability of being late?
