int xln(x) dx
1/2 x^2ln(x)-1/4x^2+C
Evaluate
int_1^2 (x + 2x^2)/x dx
Evaluate
int (4x^3) / sqrt(x^4 + 9) dx
What is
2 sqrt(x^4 + 9) + C
Evaluate
int sin(x)/root3(cos(x)) dx
What is
-3/2 (cos(x))^(2/3) + C
a) Plot the point with polar coordinates (4,2pi/3). Then find its Caresian Coordinates. b) The Cartesian coordinates of a point are -3,3. Find two sets of polar coordinates for the point.
What is
a)
(-2,2sqrt(3))
b)
(3sqrt(2), (3pi)/4)
(-3sqrt(2), (7pi)/4)
Consider the parametric equations:
x = t - 1, y = t^3
a) Eliminate the parameter to obtain an equation in terms of x and y.
b) Sketch a graph of the curve.
What is
y = (x + 1)^3
The solution to the differential equation
dy/dx = y^2 e^-x
What is
y(x) = 1/(e^-x - C)
int (x+2)e^(2x+1) dx
What is
1/2(x + 2)e^(2x + 1) - 1/4 e^(2x + 1) + C
Evaluate
int_e^(e^2) 1/(x lnx) dx
Evaluate
int tan(x) sec^4(x) dx
What is
1/4 sec^4(x) + C or 1/4 tan^4(x) + 1/2 tan^2(x) + C
Evaluate
int sin(x) cos(cos(x)) dx
What is
-sin(cos(x)) + C
Sketch the polar curve
r = 1 + cos(2theta)
. You must label all three x-intercepts in polar coordinates.

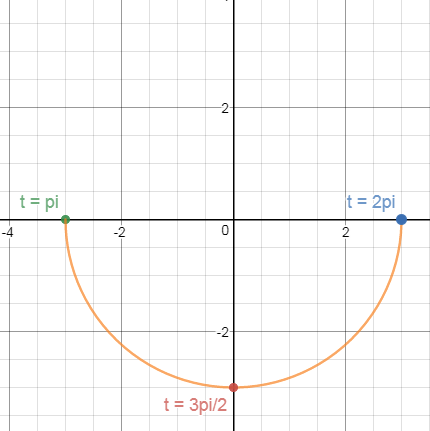
Consider the parametric equations:
x = 3cos(t), y = 3sin(t)
,
pi <= t <= 2pi
a) Eliminate the parameter to find an equation in terms of x and y.
b) Sketch a graph of the curve and indicate the direction of movement.
What is
x^2 + y^2 = 9,-3<=y<=0
The solution to the differential equation
dy/dt = (3t^2)/y
What is
y = +- sqrt(2t^3 + C)
Evaluate
int x^2 cos(x) dx
What is
x^2 sin(x) + 2x cos(x) - 2sin(x) + C
Evaluate
int_0^2 x e^xdx
What is
e^2 + 1
Evaluate
int 1/(xsqrt(lnx)) dx
What is
2 sqrt(lnx) + C
Evaluate
int tan^2(x)sec^4(x) dx
What is
1/5 tan^5(x) + 1/3 tan^3(x) + C
Find the polar equation for the curve represented by x + y = 2.
What is
r = 2/(cos(theta) + sin(theta))
Consider the parametric equations: .
x = cos(t), y = 8sin(t)
Find the equation of the tangent line to the curve at
t = pi/2
What is y = 8
The solution to the differential equation:
y' = e^(y/2) sin(t)
What is
y = -2 ln(1/2 cos(t) + C)
Evaluate
int e^sqrt(x) dx
What is
2e^sqrt(x) * sqrt(x) - 2 e^sqrt(x) + C
Evaluate
int_(sin(pi/2))^lne cos(e^(x^2))dx
Evaluate
int x sqrt(x - 5) dx
What is
2/5 (x - 5)^(5/2) + 10/3 (x - 5)^(3/2) + C
Evaluate
int (1 + cos(x))/sin(x) dx
What is
ln(csc(x) - cot(x)) + ln(sin(x)) + C
The area enclosed by the curve
r^2 = 9cos(5theta)
What is 18
The equation of the tangent line to the curve:
x = 1 + lnt, y = t^2 +2
at the point (1,3)
What is y = 2x + 1
The solution to the initial value problem:
y'(t) = e^t/(2y)
y(ln2) = 1
What is
y = sqrt(e^t - 1)
Evaluate
int e^x sin(3x) dx
What is
1/10 e^x sin(3x) - 3/10 e^x cos(3x) + C
Evaluate
int_-pi^pi x e^sin(x^2)dx
Evaluate
int sqrt(16 - x^2) dx
What is
1/2 x sqrt(16 - x^2) + 8 arcsin(x/4) + C
Evaluate
int x tan^2(x) dx
What is
x tan(x) - 1/2x^2 + ln(cos(x)) + C
Find the area of the region that lies inside both of the circles
r = 2 sin(theta)
and
r = sin(theta) + cos(theta)
What is
1/2 (pi - 1)
At what point on the curve defined by the parametric equations
x = 3t^2 + 1, y = t^3 - 1
does the tangent line have slope 1/2
What is (4,0)
The solution to the initial problem
dy/dx = e^(x-y)
y(0)=ln3
What is
y = ln(e^x + 2)