Multiplying/Dividing Polynomials
Adding/Subtracting Polynomials
Special Products
Factoring Polynomials
Miscellaneous
100
Multiply the Polynomials:
3x2 (2x4)
6x6
100
Add the Polynomials
(4x + 9) + (x - 4)
5x + 5
100
Find the product:
(-12 - n)2
n2 + 24n + 144
100
Factor the polynomial:
24x + 48y
24(x + 2y)
100
1.) Write the polynomial in standard form. 2.) Identify the degree and 3.) classify the polynomial by the number of terms.
4 + 5x2 − x
1.) 5x2 − x + 4
2.) Degree 2
3.) Trinomial
200
Multiply the Polynomials:
(4n - 1)(3n + 4)
12n2 + 13n - 4
200
Subtract the polynomials:
(g - 4) - (3g - 6)
-2g + 2
200
Find the product:
(2.5 + 3a)(2.5 - 3a)
− 9a2 + 6.25
200
Solve the equation:
(2a − 6)(3a + 15) = 0
a = 3, a = −5
200
Write the polynomial in standard form that represents the perimeter of the quadrilateral.
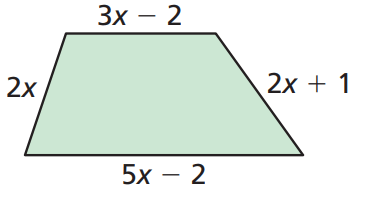
12x − 3
300
Find the quotient:
(7b + 14)/(b + 2)
7
300
Add the polynomials:
(x2 + 3x + 5) + (-x2 + 6x)
9x + 5
300
Find the product:
(2m2 - 5n2)2
4m4 - 20m2n2 + 25n4
300
Solve the equation:
4p2 − p = 0
p = 0 and 1/4
300
Solve the equation:
34x + 6 = 9x
x = −3
400
Multiply the Polynomials:
(d + 3)(d2 - 4d + 1)
d3 - d2 -11d + 3
400
Subtract the Polynomials:
(k2 + 6k3 - 4) - (5k3 + 7k - 3k2)
k3 + 4k2 - 7k - 4
400
Find the product:
(r3 - 6t4)(r3 + 6t4)
-36t8 + r6
400
Solve the equation:
6n2 = 15n
n = 0 and 5/2
400
Find the value of the variable. Then find the angle measures of the triangle.
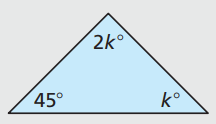
k = 45; 45°, 90°, 45°
500
Find the quotient:
(-6k^4+15k^3-9k^2)/(3k^2)
-2k2 + 5k - 3
500
Add the polynomials:
(-1 + x2 + 2x) + (1 - 2x + 2x2)
3x2
500
Find k so that 9x2 − 48x + k is the square of a binomial.
k = 64
500
Solve (4x − 5 − 16)(3x − 81) = 0
x = 7, x = 4
500
A movie theater sells 12 large bags of popcorn and 25 small bags of popcorn for $227. A large bag of popcorn costs $3.50 more than a small bag of popcorn. How much does each size cost?
small: $5, large: $8.50