8.1 - Similarity in Right Triangles
8.2 - Trig ratios
8.3 - Solving Right Triangles
8.4 - Angles of Elevation and Depression
100
Complete the similarity statement for the triangles shown:
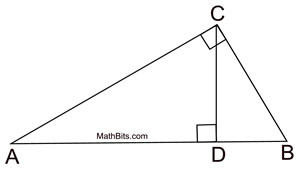
triangle ACB ~
triangle ACB ~ triangle ADC ~ triangle CDB
100
sine is the ratio of...
opposite over hypotenuse
100
Find the measure of <A in the right triangle shown:
m<A = 28
100
Angle 1 is what type of angle?

Angle of depression
200
Find the geometric mean of 6 and 8
4 sqrt(3)
200
cosine is the ratio of...
adjacent over hypotenuse
200
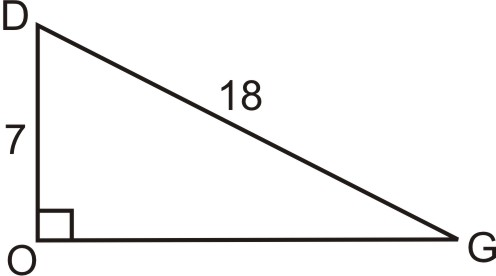
Find the length of side OG in the right triangle shown. Round your answer to the nearest hundredth.
OG is approximately 16.58
200
Angle 2 is what type of angle?

Angle of elevation
300
Solve for x in the triangle shown:

x = 7
300
tangent is the ratio of...
opposite over adjacent
300
Find the length of side AC in the figure shown. Round your answer to the nearest hundredth.

AC is approximately 8.52
300
Find the horizontal distance from the jet to the battleship. Round your answer to the nearest whole foot.
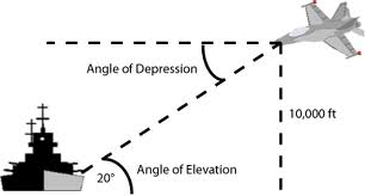
approximately 27,475 feet
400
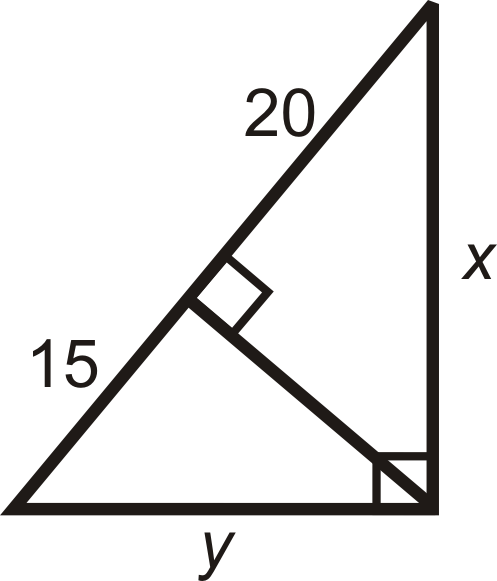
Find y in the right triangle shown:
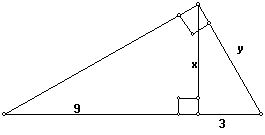
y = 6
400
Find the length of AB in the right triangle shown:
AB = 18
400
Find m<C in the right triangle shown. Round to the nearest whole degree.

m<C is approximately 37 degrees
400
Find the horizontal distance of the park ranger to the observation tower. Round your answer to the nearest whole foot.
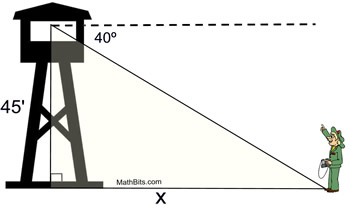
Approximately 54 feet
500
Find x in the right triangle shown:
x = 10 sqrt(7)
500
Find the length of AC in the figure shown. Round your answer to the nearest hundredth.
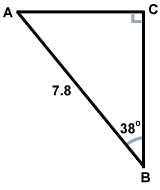
AC is approximately 4.80
500
Find m<A in the right triangle shown. Round to the nearest whole degree

m<A is approximately 53 degrees
500
An electrical engineer stands at a distance of 87 feet from a cell phone tower. The angle of elevation to the first tier is 25 degrees. The angle of elevation to the second tier is 45 degrees. What is the distance between tier 1 and tier 2? Round your answer to the nearest whole foot.
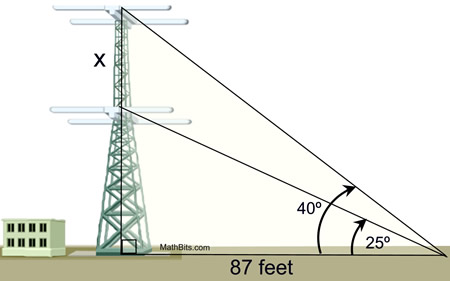
Approximately 32 feet