Show:
Circle, Circumference, Angles, and Arcs
Arcs, Chords, and Inscribed Angles
Secants, Tangents, and Angle Measures
Special Segments of in a Circle and Equations of a Circle
Micellaneous
100
Name a Chord
What is DC
100
In a circle two or more minor arcs are congruent if and only if...
What is the corresponding chords are congruent
100
True of false: If a line is tangent to a circle, then the radius is perpendicular to the point of tangency
True
100
True or False: If two chord intersect in a circle then the products of the measures of the segments of the chords are equal.
What is True
100
Find X
What is X=8
200
What is the angle formed by the hour and minute hand on a clock if the time is 7:00?
What is 210
200
In a circle or in congruent circles, two chords are congruent if and only if...
What is equidistant from the center
200
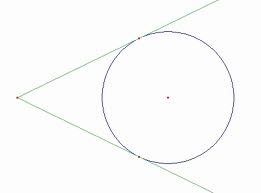True of false: If two segments from the same exterior point are tangent to the circle, then they are congruent
True
200
Is AB tangent to the circle?
What is yes
200
If the lengths of the chords are equal and the measure of the white arc is 150 then what is the measure of the red arc?
What is 150
300
Find: XB and YC
What is XB=5 and YB=3
300
What is the difference in the relationship of an inscribed angle to its arc and a central angle to its arc?
The measure of an inscribed angle is one half the measure of its arc and the measure of a central angle is equal to the measure of its arc
300
What is the value of x (round to nearest 10th)
What is 2.5
300
AC= 52 AT=18 SB=12 Find the perimeter of the triangle
What is 128
300
Circle O has a radius of 13 inches. Radius OB is perpendicular to chord CD which is 24 inches long. If the measure of arc DO= 134 find the measure of arc DC.
What is measure of arc CB= ½ (134) or 67
400
Prove that angle C=15 degrees if angle DAB=30 degrees
What is A: Given B: Arc DB=60 because the measure of the central angle equals the arc C: Angle C=30 because the measure of inscribed angles is half it's arc
400
Circle O has a radius of 13 inches. Radius OB is perpendicular to chord CD which is 24 inches long. If the measure of arc DO= 134 find the measure of OX.
What is ox=5
400
Find x
What is 3.25
400
Which statement should be swapped.
What is 2 and 3
400
Explain the difference between an inscribed polygon and a circumscribed circle.
An inscribed polygon has all vertices on the circle. A circumscribed circle means the circle is drawn around so that the polygon lies in its interior and all vertices lie in the circle.
500
If the circumference of a circle is 36, find the radius, diameter, and area.
What is Radius=3.6 Diameter=6.2 Area=72
500
Write a proof for theorem 10.2. In a circle or in a congruent circle, two minor arcs are congruent if and only if their corresponding chords are congruent. Given: Circle X, Arc UV is congruent to arc YW Prove: Line segment UV is congruent to line segment YW
1. Circle X, arc UV is congruent to arc YW 1. Given 2.Angle UXV is congruent to angle WXY 2. If arcs are congruent, their corresponding central angles are congruent 3.Line segment UX is congruent to line Segment XV which is congruent to Line segment XW which is congruent to line segment XY 3. All Radii of a circle are congruent 4. Triangle UXV is congruent to triangle WXY 4. SAS 5. Line segment UV is congruent to line segment YW 5. CPCTC
500
CONCLUSIONS - Tangents are perpendicular to radii -Tangents with common exterior points are congruent -Line CA is congruent to line CA only if circles are different sizes Based on the prrof above which conclusions are true
What is 1 and 2
500
Find the radius of a circle whose equation is (x-3)^2+(y-2)^2=r^2
What is radius equals 2.8
500
Circle O has a radius of 13 inches. Chord OD is perpendicular to chord CP which is 24 inches long. If the measure of arc DO= 134 find the measure of arc DC.
What is measure of arc CB= ½ (134) or 67