What does the Pythagorean Theorem say
and
on what kind of triangle can we apply it?
Pythagorean Theorem
a2+b2=c2
We can only use it on RIGHT triangles.
What is the name of this function?
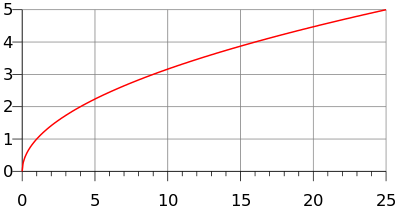
Squareroot function
or
f(x)=\sqrt(x)
Is this a polynomial function why or why not?
f(x)=x^3+ \sqrt(2)x^-2+2x+1
How do you construct a rational function?
Give an example.
It is a polynomial divided by a polynomial.
f(x)=\frac{x^2+2x}{\pix^3-5.4x+1}
What does this notation mean?
f \circ g
f hugs g
g is the input in f
f composed with g
What is the distance formula?
d=\sqrt((y_2-y_1)^2+(x_2-x_1)^2)
Is this the graph of a function why or why not?
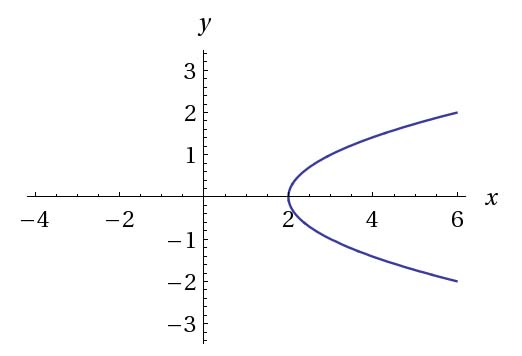
No, it does not pass the vertical line test
or
there are is one value of x for 2 values of y.
What is the degree of the following polynomial?
f(x)=x^2(x^3+x-4)
The degree is 5.
You can find this by multiplying the polynomials.
What are the steps in finding a vertical asymptote of a rational function?
Step 1: Factor polynomials and eliminate common factors.
Step 2: Make denominator equal to zero and solve for the given variable.
For example: x=3 ( vertical line at x value 3)
What are the steps in finding the inverse functions?
1. Let f(x) equal to y
2. Switch the x and y
3. Solve for y
4. Replace y with the inverse notation
f^-1(x)
What is the midpoint formula?
m=(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})
Parent function is
f(x)=x^2
Apply the following transformations and come up with one function.
1. Reflected about the x-axis
2. Shifted up 2 units
3. Shifted left 3 units
f(x)=-(x+3)^2+2
How does the degree of the function relate to the end behavior of the graph?
If the degree is even
the end behaviors will BOTH point to positive or negative infinity.
If the degree is odd
the end behaviors will point to opposite directions.
Is it possible to have a horizontal asymptote and a slant asymptote, why or why not?
It is NOT possible because in order to have a horizontal asymptote
the degree of my numerator needs to be equal or smaller than the degree of my denominator.
In order to have a slant asymptote the degree of my numerator needs to be one more than the degree of my denominator
If we plot a function and its inverse on the same graph how can we tell we are correct?
The will be symmetric with respect to the identity function
y=x
Find all points having an x- coordinate of 3 whose distance from the point (-2,-1) is 13.
(3,-13), (3,11)
Parent function is
f(x)=\abs(x)
Find the function with the following transformations.
1. Reflected across the y-axis
2. Reflected across the x-axis
3. Shifted right 4 units
4. Shifted down 7 units
f(x)=-\abs(-x+4)-7
What is the multiplicity of the following factors and how does that affect the graph?
f(x)=x(x-2)^2(2x+3)^5
x has multiplicity 1
- the graph will cross that zero(x-intercept)
(x-2) has multiplicity 2
- the graph will bounce of that zero (x-intercept)
(2x+3) has multiplicity 5
- again since it it odd the graph will cross that zero (x-intercept)
Find the H.A, V.A and or S.A of the following rational function.
R(x)=\frac{x}{(x-1)(x-2)}
H.A : y=0 since the degree of the numerator is less than the degree of my denominator.
V.A: x=1 and x=2
S.A: no S.A because we have an H.A.
Find the domain of f and the inverse.
f(x)=ln(x+4)
The domain:
{x|x > -4}
The inverse is:
f^-1(x)=e^x-4
Derive the distance formula on the board.
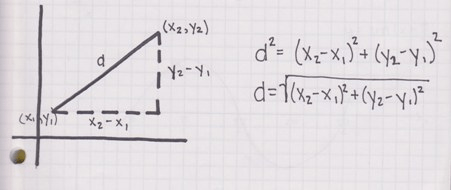
Find the domain and range of this function:
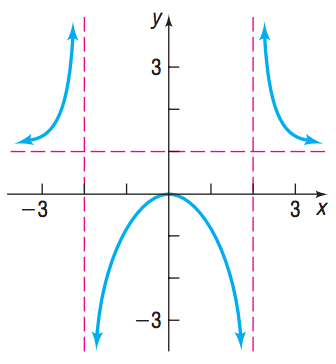
Domain:
(-infty,-2)\cup(-2,2)\cup(2,\infty)
Range:
(\infty,0]\cup (1,\infty)
Construct a polynomial function that might have the given graph.
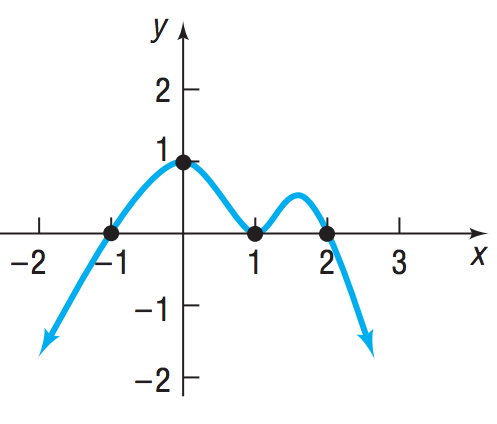
f(x)=-(x+1)(x-1)^2(x-2)
Find the S.A of the following rational function.
R(x)=\frac{(x-1)(x+1)}{x}
S.A: y=x
Write as a single logarithm.
3log_5(3x+1)-2log_5(2x-1)-log_5x
log_5\frac{(3x+1)^3}{(2x-1)^2x}