Calculate P5
5! =5·4·3·2·1=120
Peter must choose one of 3 appetizers, one of 6 main courses and one of 5 different desserts to have lunch. How many different meals can he order?
3·6·5= 90 different meals
Write with mathematical notation the sample space of the next random experiment: flipping a coin twice.
E={HH,HT,TH,TT}
I've rolled a biased die 1000 times, of which I've gotten the number six 347 times. What is the probability of getting a six on the next roll?
347/1000=0.347
In a bag there are 3 red balls and 7 green balls. You take out two marbles from the bag. What is P(R 2nd/G 1st)?
3/9=1/3
Calculate V6,3
6·5·4=120
A pizza place offers 7 different toppings. How many different four topping pizzas can you order?
C_{7,4}=(7!)/(4!3!)=(7·6·5)/(3!)=7·5=35
toppings
We roll a die and we define the following events: A = {1,2,3} and B = "greater than 3". Are A and B incompatible?
Yes, because A
A cap B = emptyset
What is the probability of picking an ace or a king from a Spanish deck?
8/40=1/5
In how many different ways can you answer a 5 question true or false quiz?
2 · 2 · 2 · 2 ·2 or 2^5 =32 ways
Calculate VR3,5
3^5=243
A school newspaper has an editor-in-chief and an assistant editor-in-chief. If the newspaper staff has 15 members, in how many different ways can these positions be filled?
V_{15,2}=15 · 14=210
We roll a die. If we define the events A = {3,5} and B = "greater than 4", determine (A U B)'.
(A U B)'={1,2,4}
In a bag there are five red balls and six green balls. You take out two balls from the bag. What is the probability that you take different colour balls?
5/11·6/10+6/10·5/11=30/110+30/110=60/110=6/11
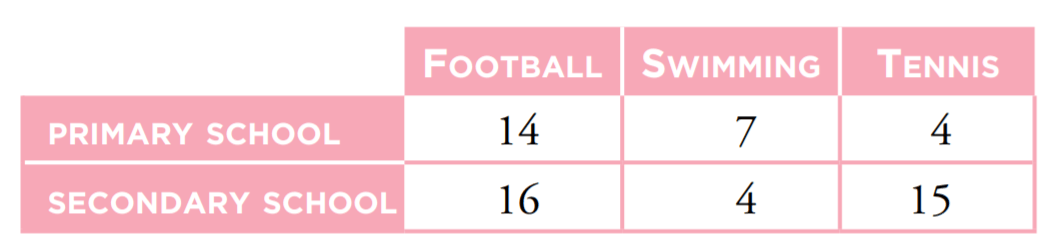
Calculate the probability that a student plays tennis given that the student is in secondary school.
15/35=3/7
Calculate C8,5
(8!)/(5! 3!)=(8·7·6)/(3!)=8·7=56
In Spain, license plates are made up of 4 numbers followed by 3 letters. If the letters cannot be vowels (A,E,I,O,U), neither Ñ nor Q, how many different license plates are possible?
VR_{10,4}·VR_{20,3}=10^4·20^3=80000000
We roll a die. If we define the following events: A = {even}, B = "less than 4", C = {1,6}, find the event (A U B) ∩ C
(A U B) ∩ C ={1,6}
You roll two dice. What is the probability that their product is a multiple of 3?
20/36=5/9
(Hint: make a table of products)
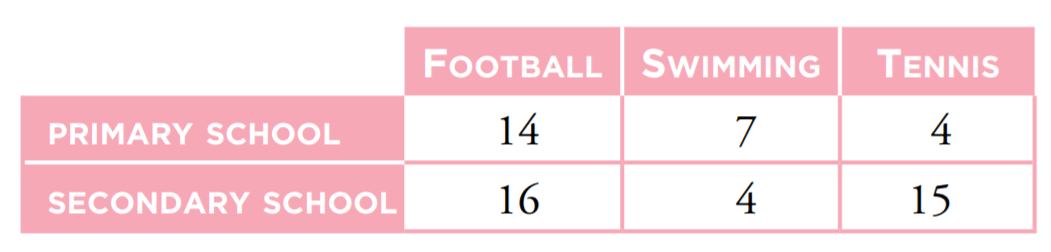
Calculate the probability of playing tennis and being in secondary school.
15/60=1/4
(V_{8,6})/(P_6)
(8·7·6·5·4·3)/(6·5·4·3·2·1)=4·7=28=C_{8,6}
A box contains 10 black and 5 green balls. In how many different ways can you choose 8 black balls and 3 green balls?
C_{10,8}·C_{5,3}=45·10=450
If A and B are two events, the opposite of their union is equal to the intersection of...
(AUB)'= ? cap ?
(AUB)'= A' cap B'
Morgan's law
In a bag there are five red balls numbered from 1 to 5 and eight blue balls numbered from 1 to 8. You take out two balls from the bag. What is the probability that you take a blue odd-numbered ball first, and that the second ball is a multiple of 4?
4/13 · 3/12= 4/13 · 1/4 = 1/13
You toss 4 coins. What is the probability that 3 or more of them are heads?
5/16