Proof Reasons
Are they congruent
Name that angle relationship
Quadrilaterals
100
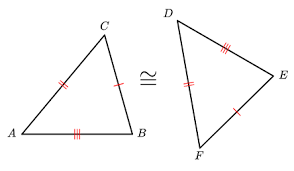
Triangle ACB is congruent to triangle DFE. Explain how we know this is true.
They are congruent by SSS.
100
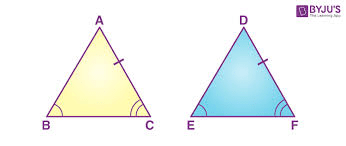
Are triangles ABC and DEF congruent? If so, by what theorem or postulate?
Yes, AAS
100
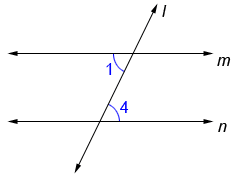
What is the angle relationship between angle 1 and angle 4?
They are alternate interior angles.
100
True or False:
All rectangles are squares
False.
200
In the following image, what property allows me to say that IJ ≅ IJ?
The reflexive property.
200
Are triangles ABC and DEF congruent? Explain how you know
Yes, by HL
200
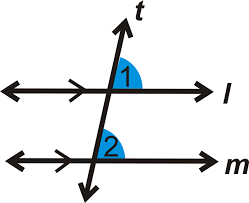
What types of angles are angles 1 and 2?
Corresponding
200
True or false:
If a shape has 4 equal sides, then it must be a square
False
300
If
∠1 ≅ ∠2
∠2 ≅ ∠3
Why can we then say that ∠1 ≅ ∠3?
Transitive Property
300
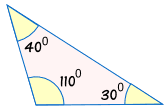
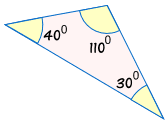
Can we prove that these two triangles are congruent? Explain you reasoning.
No, knowing that all angles are the same is not enough information to prove two triangles congruent.
No, AAA does not work.
300
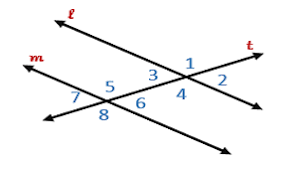
What type of angles are angles 1 and 7? Are they congruent or supplementary?
They are same-side exterior angles. They are supplementary.
300
True or False:
Some parallelograms are squares
True.
400
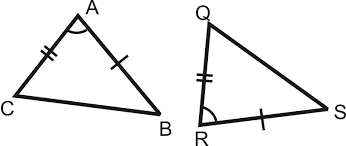
Write a congruence statement for these two triangles. Explain how you know they are congruent.
Triangle ABC is congruent to triangle RSQ
SAS
400
Given the picture above, do we have enough information to prove that these triangles are congruent? What other information would we need?
No,
We would need either two sides, or another angle and a side
400
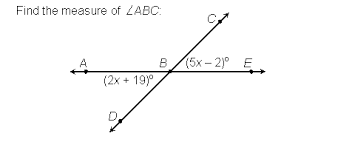
What is the relationship between angle ABD and angle EBC?
Use this relationship to solve for x. Show or explain your work.
Vertical Angles
x = 7
400
The following claim is false:
The diagonals of all quadrilaterals bisect each other.
Provide a counterexample that shows this is false.
A trapezoid, a kite, any quadrilateral that is not a parallelogram
500
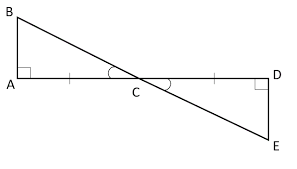
Given the information above, why are triangles ABC and DEC congruent?
Why is line segment DE congruent to line segment AB?
ASA
CPCFC (corresponding parts of congruent figures are congruent)
500
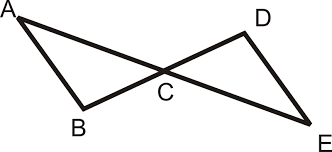
C is the midpoint of AE and DB. Are the triangles congruent? Explain how you know.
Yes, because of SAS. C being the midpoint makes AC equal to EC and BC equal to DC. Angle ACB is congruent to angle DCE because they are vertical angles.
500
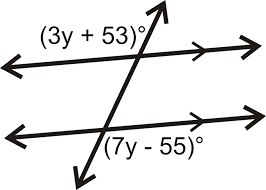
What is the relationship between the two angles shown?
Use that relationship and solve for y. You must show your work.
Alternate Exterior Angles
y = 27
500
A quadrilateral has diagonals that are perpendicular bisectors of each other. List all the quadrilaterals this could be.
Parallelogram, rhombus, square, rectangle