Parallelogram Properties
Triangle Congruence Theorems
Name the Reason
Proofs
Miscellaneous
100
What is the definition of a parallelogram?
A quadrilateral with both pairs of opposite sides parallel.
100
Which triangle congruence theorem applies?
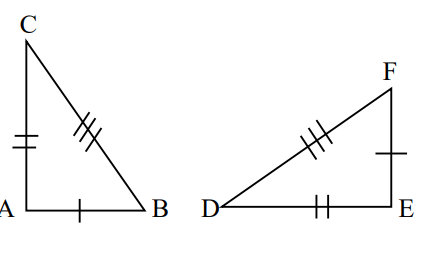
Side-Side-Side (SSS)
100
The reason that goes with this step
AB=AB
Reflexive Property
100
Complete the proof.
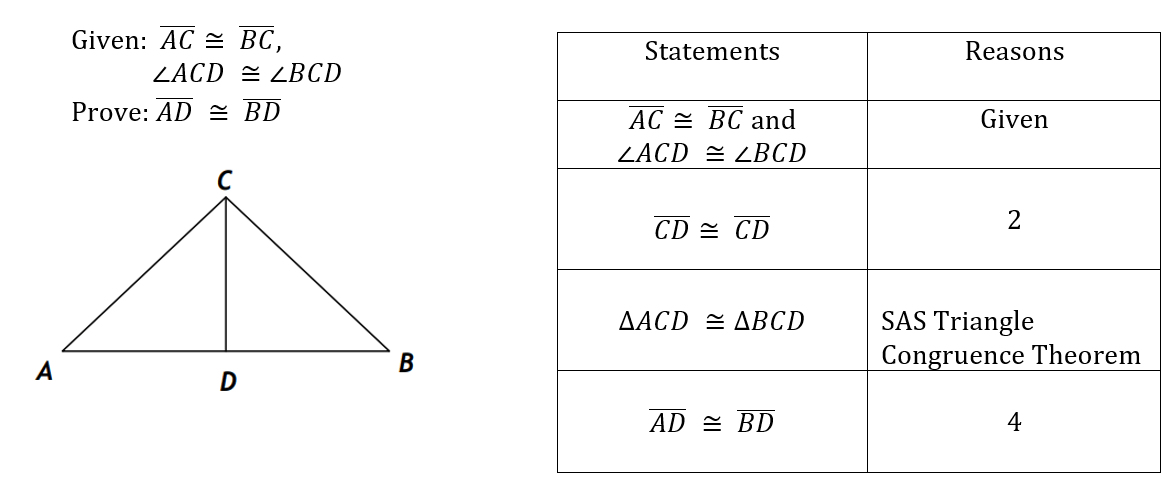
2. Reflexive Property
4. Corresponding Parts of Congruent Triangles are Congruent
100
Given the congruence statement, what angle on the other triangle is congruent to angle B?
\triangleACB\cong\triangleYXZ
angle Z
200
Given segment AD is 6 cm, what is the length of segment BC?
6 cm
200
Which triangle congruence theorem applies?
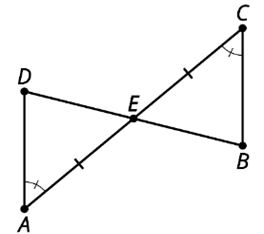
Angle-Side-Angle (ASA)
200
The justification for this step:
∠BCA ≅ ∠ECD
Vertical Angles
200
Complete the proof.
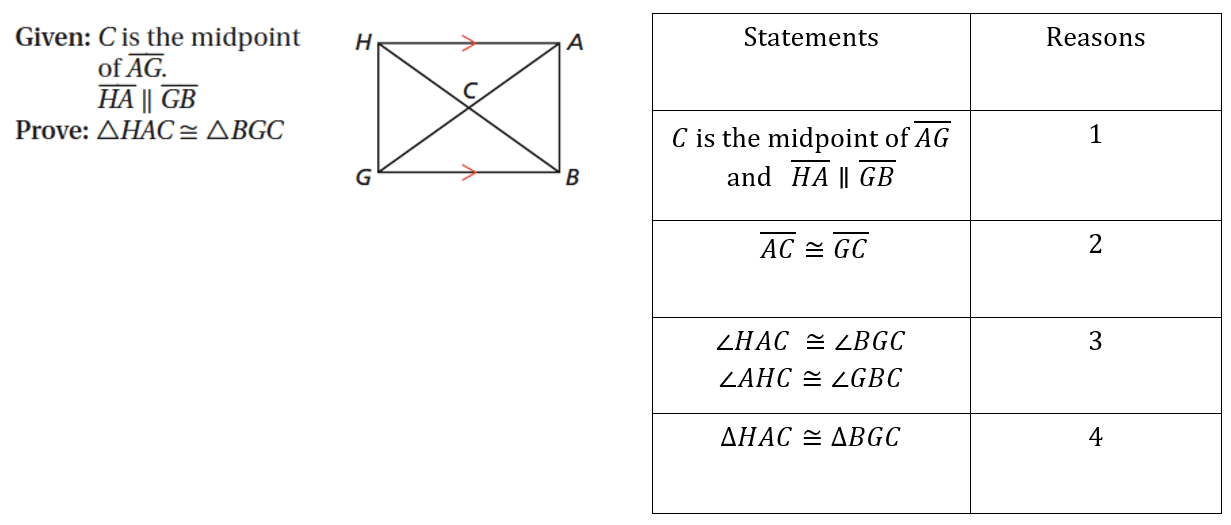
1. Given
2. Definition of midpoint
3. Alternate Interior Angles Theorem
4. Angle-Angle-Side Triangle Congruence Theorem
200
Line ZO is the perpendicular bisector of segment XY. What is one statement that can be written about the segments or angles in the diagram based on this information?
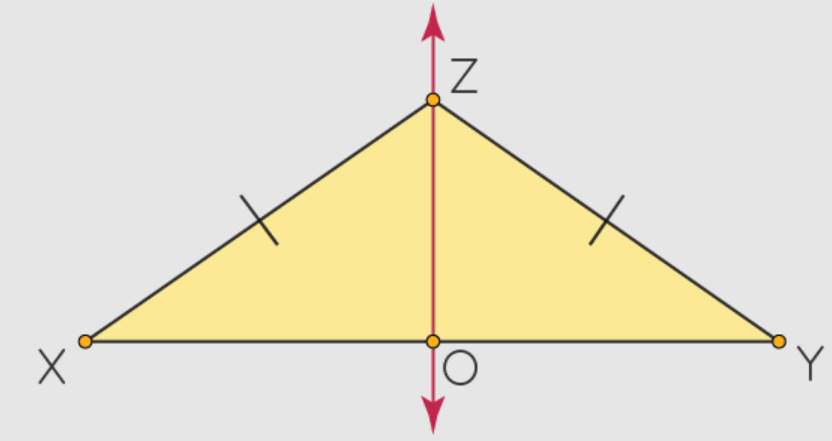
Segment XO and segment YO are congruent.
Angles XOZ and YOZ are right angles.
300
In parallelogram ABCD, the measure of angle A is 25°.
What is the measure of angle C? Explain how you know.
Angle C measure 25° because opposite angles in a parallelogram are congruent.
300
Name the five triangle congruence theorems.
Side-Angle-Side (SAS)
Angle-Side-Angle (ASA)
Angle-Angle-Side (AAS)
Side-Side-Side (SSS)
Hypotenuse-Leg (HL)
300
C is the midpoint of AE.
The justification for this step:
AC≅CE
Definition of midpoint
300
Complete the proof.
Mrs. V will check!
300
The measure of angle R is 57°. Find the missing angle measures.
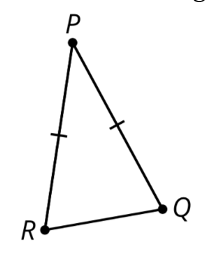
m\angleQ = 57°
m\angleP = 66°
400
What are the values of x, y, and z?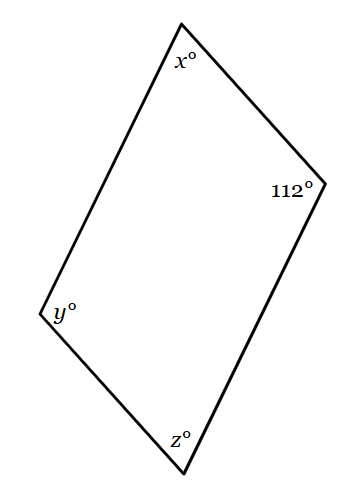
x = 68, y = 112, z = 68
400
What additional information would be needed to prove the triangles are congruent using SAS Triangle Congruence Theorem?
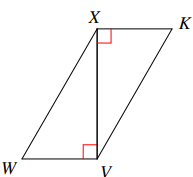
\bar{WV}\cong\bar{KX}
400
Given:
AE bisects BD
The parts of the triangle that are now congruent:
What is
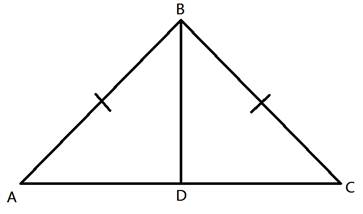
BC = CD
400
ABC is an isosceles triangle. AD is the angle bisector of ∠BAC
Mrs. V will check!
400
If the measure of angle 1 = 146, find the measure of angles 2, 3, and 4.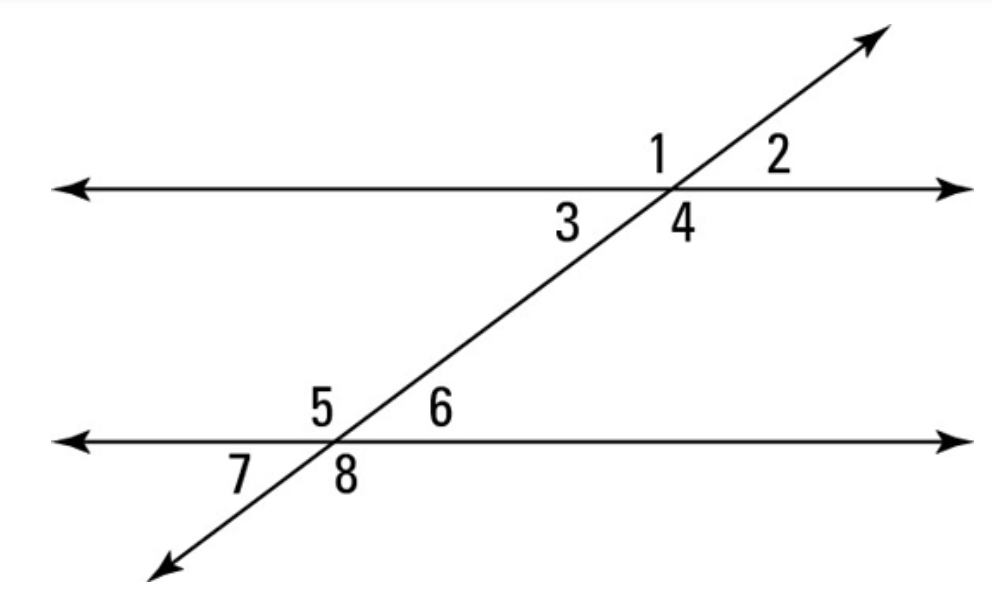 
34, 34, 146
500
In parallelogram EFGH, the measure of angle E is 33°.
What is the measure of angle H? Explain how you know.
Angle H measures 147° because angle E and angle H are supplementary by the Same Side Interior Angles Theorem which means their angle measures sum to 180 degrees.
500
Write the corresponding triangle congruence theorem and complete the congruence statement.
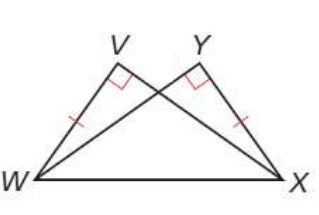
\triangleWVX\cong\triangle
Hypotenuse-Leg (HL)
\triangleWVX\cong\triangleXYW
500
Given:
BD bisects ∠ABC
The parts of the triangle that are now congruent
∠ABD = ∠CBD
500
Figure KLMN is a parallelogram. Prove that triangle KNL is congruent to triangle MLN.
Figure KLMN is a parallelogram. By the definition of a parallelogram, \bar{KN}∥\bar{ML} and \bar{NM}∥\bar{KL} . \angleKLN\cong\angleMNL and \angleKNL\cong\angleMLN by the Alternate Interior Angles Theorem. \bar{NL}\cong\bar{NL} by the reflexive property. Therefore \triangleKNL\cong\triangleMLN by the Angle-Side-Angle Triangle Congruence Theorem.
500
Which step has an error? Explain why.
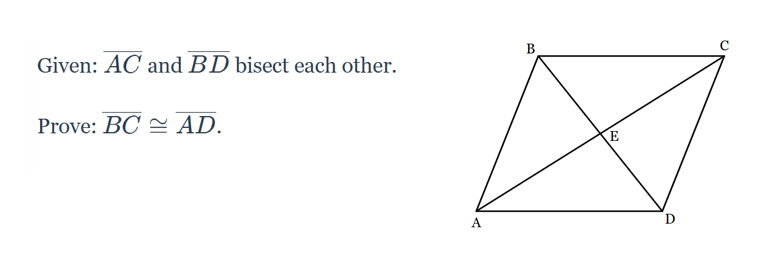
Step 4 has an error because it has not justified that the included angles between the two pairs of congruent sides are congruent. Before step 4, it should be stated that angle BEC and angle DEA are congruent by the Vertical Angles Theorem.