Transformations
Circles
Parabolas
Equations of Lines
Miscellaneous
100
Describe the transformation defined by the rule (x,y) -> (x+1, y+1).
Translation by the directed line segment from (0, 0) to (1, 1) OR Translation right 1 unit and up 1 unit
100
Find the center and radius of the circle given by the following equation.
(x-3)^2+(y+5)^2=36
center: (3, -5)
radius: 6
100
A parabola has focus (1, 3) and directrix y =-7. Determine the distance between the focus and point P given point P is on the parabola and 2 units from the directrix.
2 units
100
Write the equation of the line passing through point (-3, 4) with slope 1/2 .
y-4=1/2(x+3)
100
Find the distance between (6, 17) and (9, 15).
sqrt13
200
The points P(5,-9), Q(9, -2), R (2,-3) form triangle PQR. Find the coordinates of the image under the rule (x,y)->(x,-y) .
P': (5, 9)
Q': (9, 2)
R': (2, 3)
200
The point (8, -1) is on a circle with center (4,2). Write the equation of the circle.
(x-4)^2+(y-2)^2=25
200
A parabola has focus (2, 6) and directrix y = -4. Find the parabola’s vertex.
(2, 1)
200
What is the slope of a line parallel to y=2/3x+8?
2/3
200
Find the point that partitions segment AB in a 2:1 ratio.
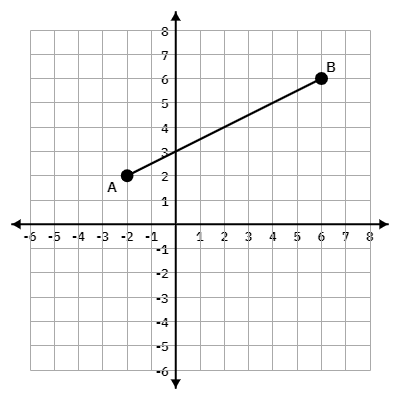
(10/3, 14/3)
300
Write a rule that describes this transformation.
(x-3) -> (x-3, -y)
300
Find the center and radius of the circle given by the following equation.
x^2-5x+25/4+y^2+24y+144=16
center:
(5/2, -12)
radius: 4
300
Write an equation that states (x, y) is the same distance from (5,4) as it is from the line y = 1.
(x-5)^2+(y-4)^2=(y-1)^2
300
Write the equation of the line perpendicular to y+1=2(x-1) passing through (-5, 2).
y-2=-1/2(x+5)
300
The points A(-7,3), B(-3, -9), C (0, -8), D(-4, 4) form rectangle ABCD. Find the area of the rectangle.
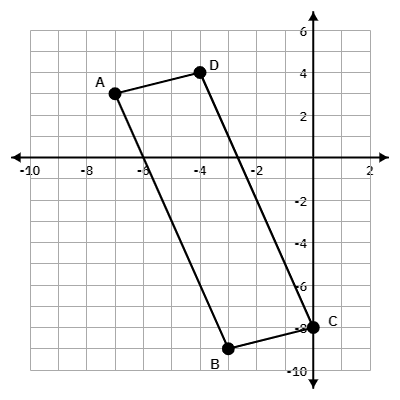
40 square units
400
Determine whether the transformation rule represents a rigid transformation, a similarity transformation, or neither.
(x,y)->(4x,3y)
neither
400
Find the center and radius of the circle given by the following equation.
x^2+y^2-18x-14y+66=0
center: (9,7)
radius: 8
400
A parabola has focus (-1, 6) and directrix y = 4. Determine whether the point (1, 7) is on the parabola. Explain your reasoning.
No. The point is 3 units from the directrix and
sqrt5
units from the focus, so it is not on the parabola.
400
The image shows the line q. Write the equation of the line parallel to q that passes through (-4, 4).
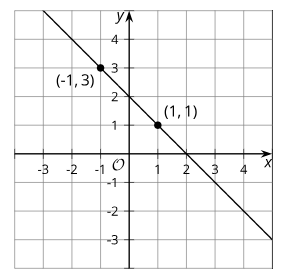
y-4=-(x+4)
400
The points A(2,3), B(5, -1), C (10,11) form triangle ABC. Find the perimeter of the triangle. Round to the nearest thousandth.
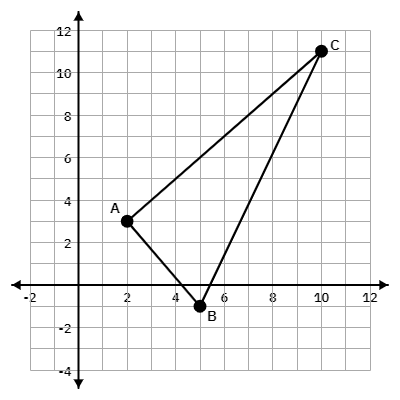
29.314 units
500
Select all the transformation rules that produce a congruent image.
a. (x, y)->(-y, x)
b. (x, y)->(2x,2y)
c. (x,y)->(x+5, y-2)
d. (x,y)->(x,y)
e. (x,y)->(-2x,5y)
a, c, d
500
Circle O has center (-1,-2) and radius 7 units. Select all points that lie on the circle.
a. (-1, 5)
b. (3, 4)
c. (2, -8)
d. (6, -2)
a,d
500
A parabola has its focus at (6,3). Its directrix is the line y = 1. Select all of the statements that are true.
a. The equation (x-6)^2+(y-3)^2=y^2 represents this parabola.
b. The equation (x-6)^2+(y-3)^2=(y-1)^2 represents this parabola.
c. The point (9,4) is on the parabola.
d. If point (x,y) is on the parabola, then the distance between (x,y) and the point (6,3) is the same as the distance between (x,y) and the line y=1.
b,d
500
Select all lines perpendicular to the line y-7=5/3(x-1) .
a. 3y=-5x+9
b. y-9=-3/5(x-3)
c. -3x + 5y = 6
d. y=-6/10x+2
b, d
500
The points A (-6, 0), B (-5, -4), C (-1, -3), and D (-2, 1) form a quadrilateral which is graphed below. Prove quadrilateral ABCD is a square.
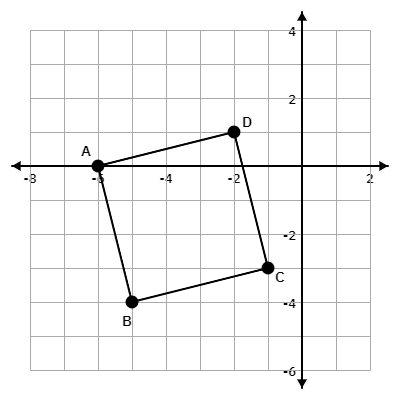
The slopes of the sides AB, BC, CD, and DA are -4, 1/4, -4, and 1/4, so each pair of intersecting sides is perpendicular. That means the quadrilateral has four right angles. All four sides have length
sqrt17
units so they are equal. Since quadrilateral ABCD has four right angles and all four sides are the same length, it is a square.