Vocabulary & Formulas
Simple and Compound Probabilities
Venn Diagrams and Two-Way Tables
Tree Diagrams
Mixed Bag
100
Events that cannot happen at the same time.
Mutually Exclusive Events
100
Suppose you spin a spinner with four equal sections (red, blue, green, and yellow) two times.
How many possible outcomes are in the sample space? Write out the sample space.
16
RR RB RG RY
BR BB BG BY
GR GB GG GY
YR YB YG YY
100
Of Mrs. Poole's 70 students, 30 play an instrument, 18 play a sport, and 7 do both. Create a Venn Diagram to display the data and then find the Probability that a student does not play an instrument.
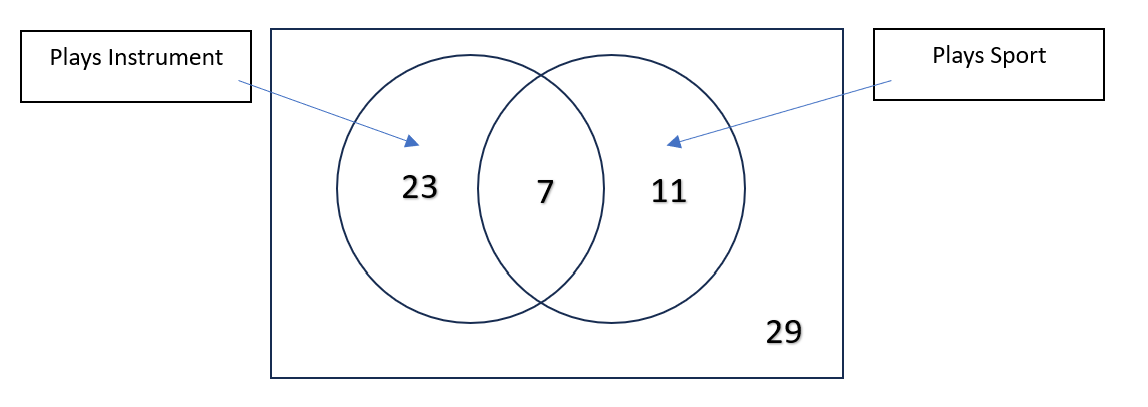
40/70=4/7
100
Use the following tree diagram to d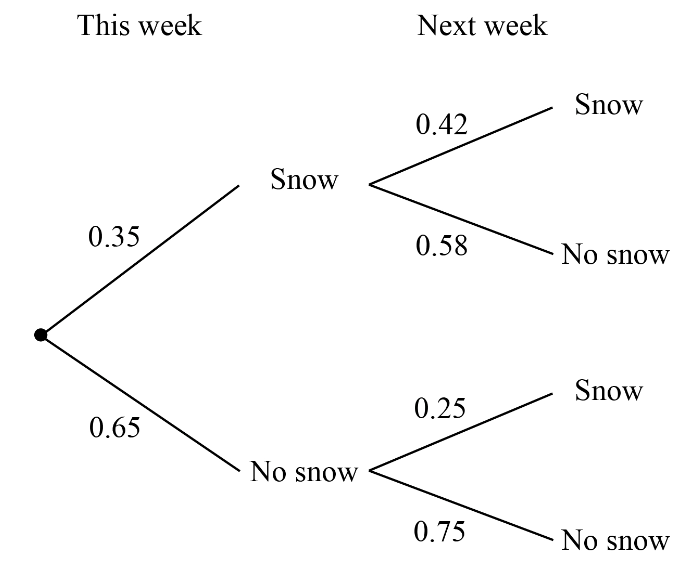
etermine the probabilty that it snows two weeks in a row.
(0.35)*(0.42)=0.147
100
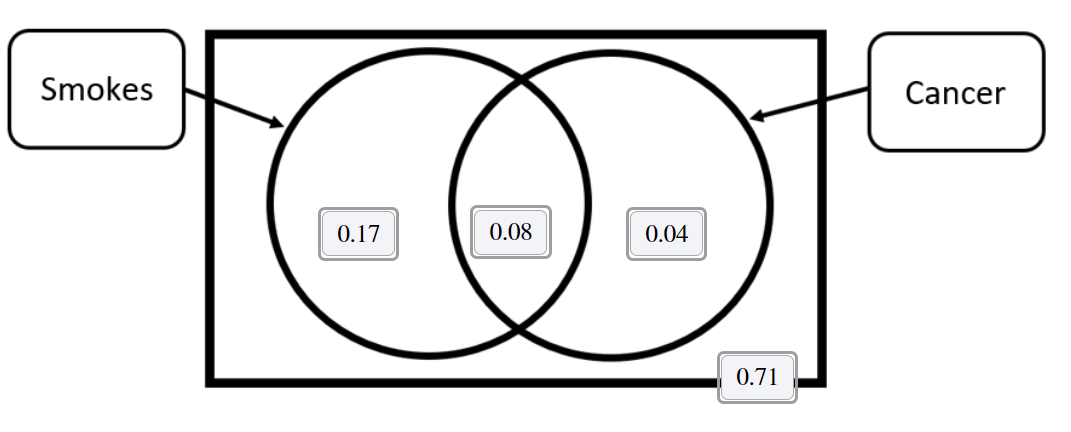
Use the following diagram to determine the probability that the individual gets cancer given that they are a smoker.
Round your answer to 2 decimal places.
Leave your answer in decimal form.
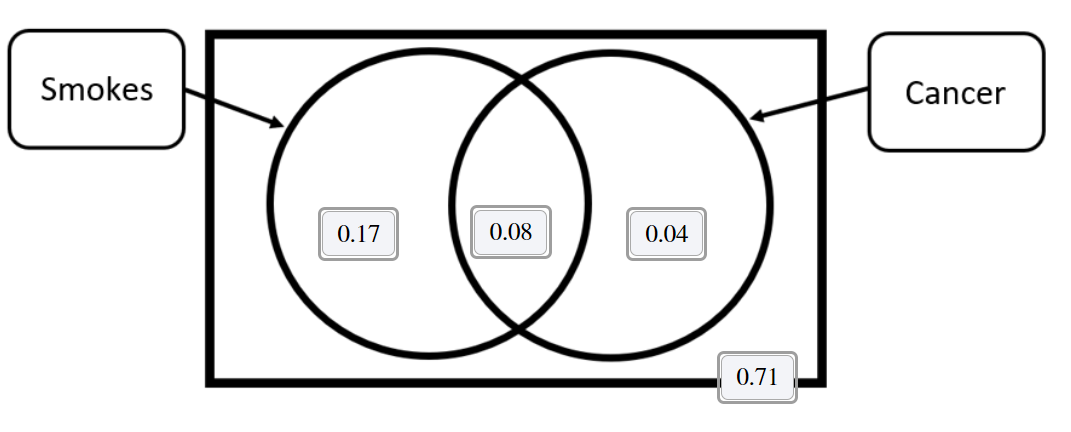
P(gets cancer|smokes)=0.32
0.08/(0.17+0.08)=0.32
200
Any collection of outcomes from some chance process.
Event
200
Suppose you spin a spinner with four equal sections (red, blue, green, and yellow) two times.
What is the probability that you land on the same color for both spins?
4/16 or 1/4
200
Use the following data to determine the probability of a student who prefers Honeybee Coffee given the student is a female.
P(Honeybee|Female)=
176/472=0.373
200
Use the following tree diagram to determine the probability that it will snow next week.
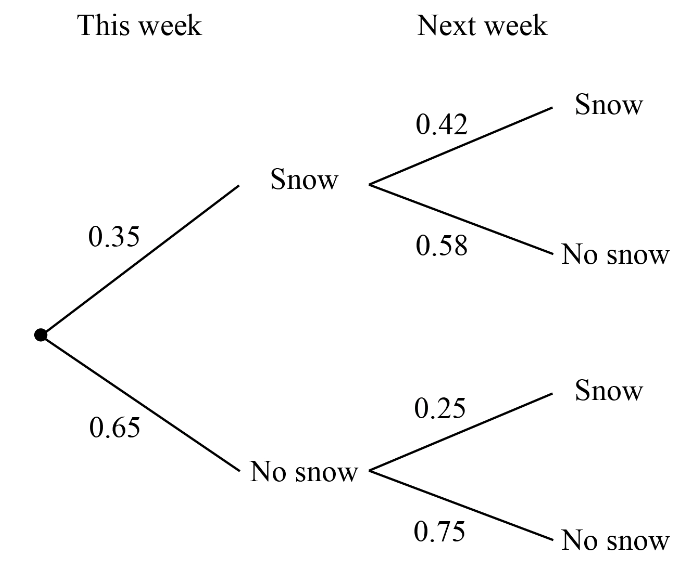
P(Snow next week)=
(0.35)(0.42)+(0.65)(0.25)=0.3095
200
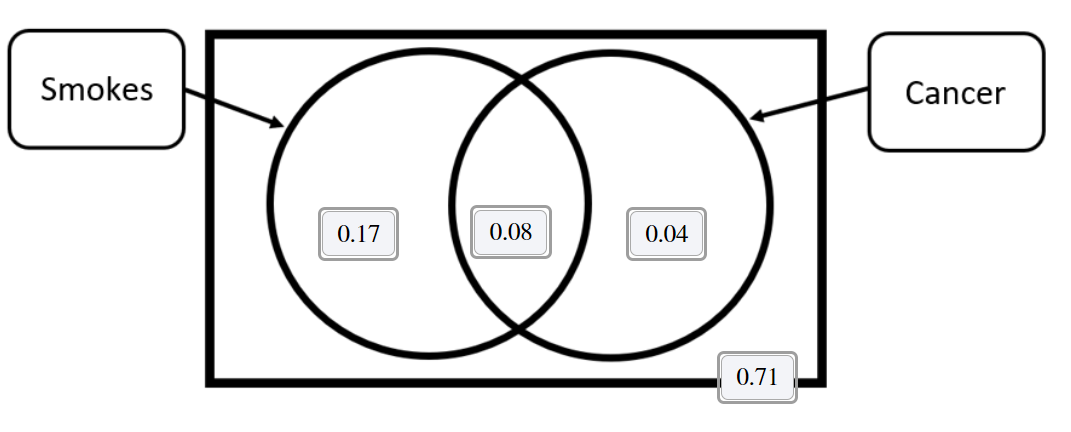
Find the probability that the individual smokes or gets cancer.
Round your answer to 2 decimal places.
Leave your answer in decimal form.
P(smokes or cancer)= P(smokes) +P(cancer)- P(both)
0.25+0.12-0.08=0.29
300
A list of all possible outcomes from a chance process.
Sample Space
300
A coin is tossed and a standard 6-sided die is rolled simultaneously. What is the probability of getting heads and rolling an even number?
1/2*3/6=3/12=1/4
300
Use the two-way table below to determine the probability that a person prefers Starbucks coffee.
P(Starbucks)=
373/770=0.484
300
Use the tree diagram to determine the probability that it doesn't snow next week.
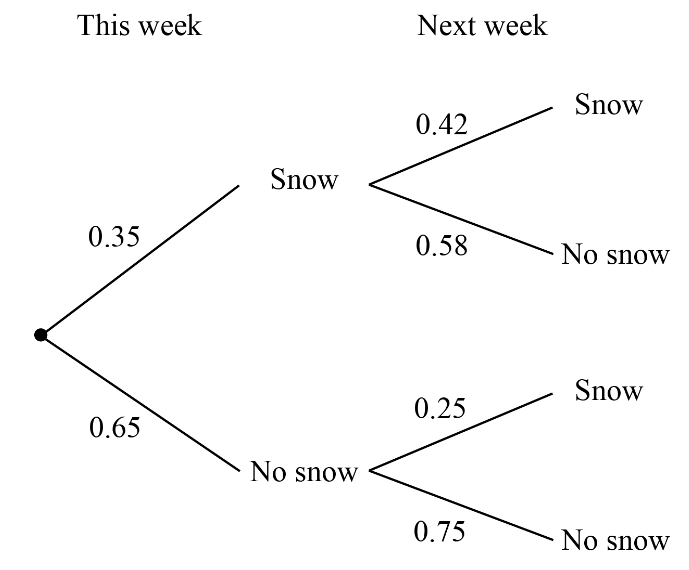
P(doesn't snow next week)=
(0.35)(0.58)+(0.65)(0.75)=0.6905
300
Two adults are selected at random. Find the probability that at least one of the two smokes.
Round your answer to 4 decimal places.
Leave your answer in decimal form.
P(at least 1)=1-P(none)
400
The name and formula for determining when an event does not happen.
Complement
P(AC)=1-P(A)
400
A bag contains 2 Snickers, 3 Reese's Cups, and 4 packs of M&M's. What is the probability of picking two candies at random without looking and without replacement and not getting a Snicker's bar?
7/9*6/8=0.583
400
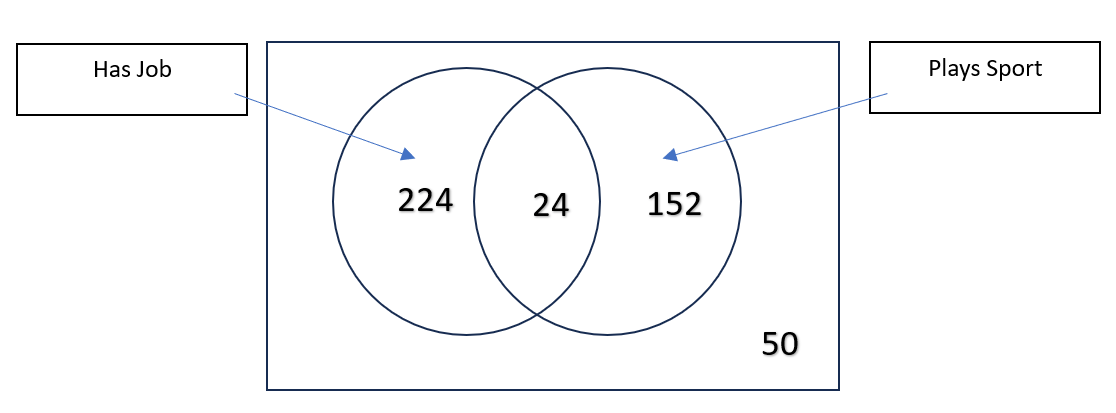
Out of 450 college students surveyed, 248 reported having a job and 176 played a sport. Fifty students reported they neither play a sport or have a job. Create a Venn Diagram to display the data. Then, find the probability that a student has a job given that they play a sport.
P(Job|Sport)=
24/176=0.136
400
Suppose that 10% of adults belong to health clubs, and 40% of these health club members go to the club at least twice a week.
Find the probability that a randomly selected adult belongs to a health club and goes there at least twice a week.
400
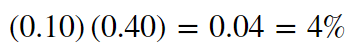
What is the probability that a randomly selected senior drives a truck?
P(truck)=1-P(not truck)
500
If knowing whether or not one event has occurred does not change the probability that the other event will happen the two events are considered ____________. What is this called and write the formula.
Independent Events
P(A|B)=P(A|BC)
500
A spinner has equally likely outcomes of Orange, Black and Purple. If someone spins the spinner and rolls a standard six-sided die, find the following probability. Let the events O, B, and P refer to the colors on the spinner and event G means rolling a number greater than 2.
P(OC and G)
P(not orange and number greater than 2)=
P(not Orange) * P(number >2)=
2/3*4/6=8/18=4/9
500
Given the two-way table below, determine the probability that a randomly selected person is female or prefers Honeybee coffee.
P(Female or Prefers Honeybee)= P(Female) + P(Honeybee) - P(Female and Honeybee)
472/770+241/770-176/770=537/770 =0.697
500
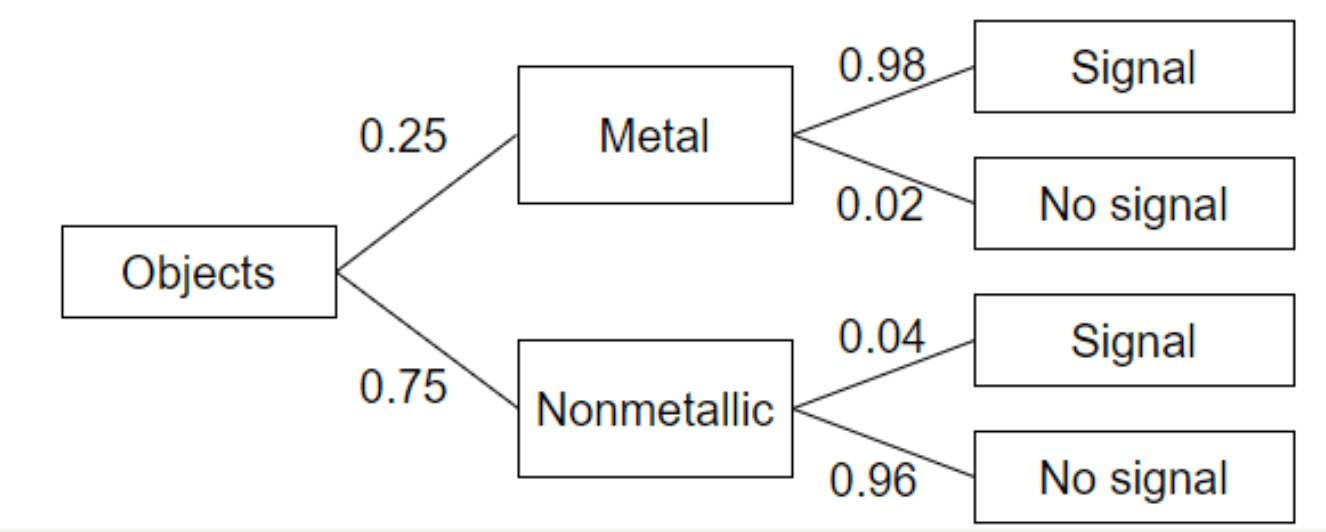
A boy uses a homemade metal detector to look for valuable metal objects on a beach. The machine isn’t perfect—it detects only 98% of the metal objects over which it passes, and it detects 4% of the nonmetallic objects over which it passes. Suppose that 25% of the objects that the machine passes over are metal. Choose an object from this beach at random. If the machine gives a signal when it passes over this object, find the probability that the boy has found a metal object.
Create a tree diagram to display the data and find the probability that the boy has found a metal object if the machine gives a signal when it passes over the object.
P(metal|signal)=
500
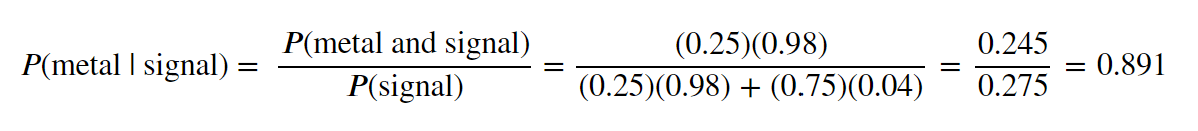
Given the table below determine the probability that a senior owns a sedan or an SUV.
P(sedan or SUV)= 0.58+0.31=0.89