an illustration that uses overlapping circles to show the logical relationship between 2+ sets of data sets.
venn diagram

How many students were included in the data?
13
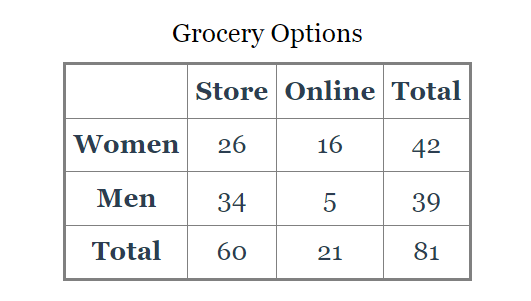
How many women were surveyed?
42
When you see the phrase "given that" in a probability problem what does it do?
limits the total(denominator) number of subject your looking at
What are the two ways to prove that events are independent?
P(A | B) = P(A)
p(A nn B) = P(A) * P(B)
a combination of two or more sets that includes ALL the elements from all sets.
union

How many students have names with 3 letters?
7
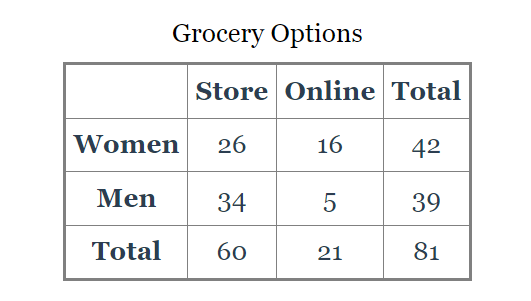
How many women did their grocery shopping in store?
26
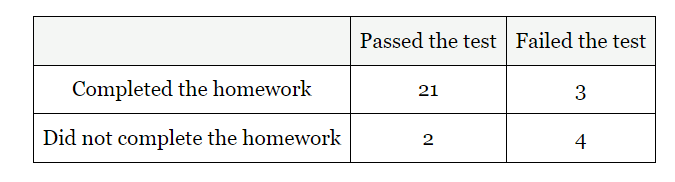
What is the probability that a student failed the test given that they completed the homework?
3/24
1/8
13%
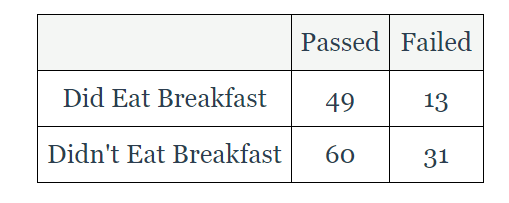
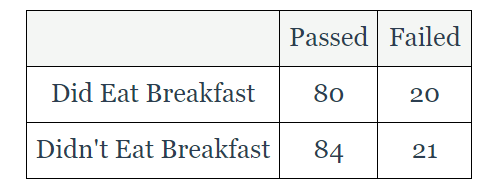
Determine if not eating breakfast and passing the test are independent events.
P(didn't eat breakfast | fail) = ______
P(didn't eat breakfast) = ____________
Independent or dependent?
.705 or 31/44
.595 or 91/153
dependent
nnn
intersection

("names ending with y" uu " names starting with A")
{Allison, Alex, Andy, Ally, Ann, Avi, Amy, Jimmy, Carly, Guy, Ivy}
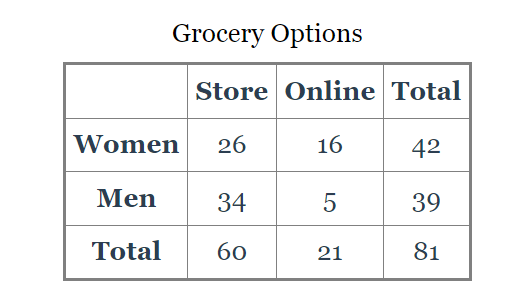
How many total people were surveyed?
81
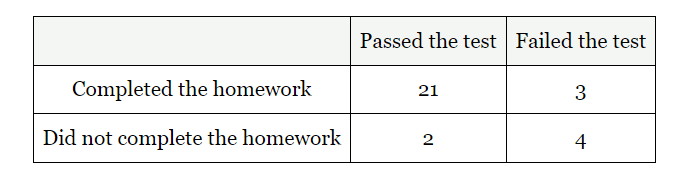
What is the probability that a students completed the homework given that they passed the test?
21/23
91%
Determine if eating breakfast and passing the test are independent.
P(did eat breakfast | pass) = ________
P(did eat breakfast) = ____________
Independent or dependent?
.488 or 80/164
.488 or 100/205
independent
the collection of elements that are NOT in a set
complement

("names ending in y" nn "names with 3 letters")
{Amy, Guy, Ivy}
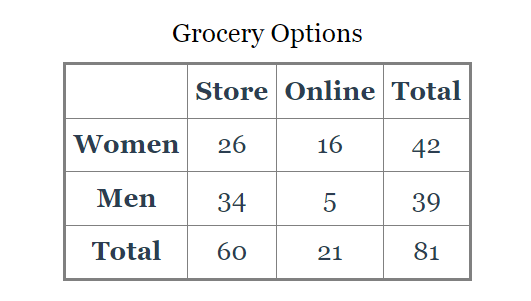 What is the probability that a person chosen randomly shops online?
What is the probability that a person chosen randomly shops online?
21/81
26%
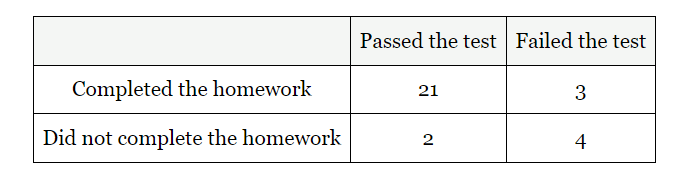
What is the probability that a student passed the test given that they did not complete the homework?
2/6
1/3
33%
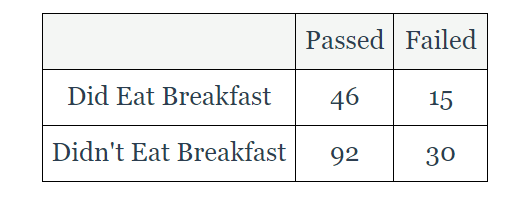
Determine if eating breakfast and passing are independent events.
P(pass | didn't eat breakfast) = _________________
P(pass) = ___________________
independent or dependent?
.754 or 92/122
.754 or 138/183
independent
uuu
union

(Names starting with A)'
{Jimmy, Carly, Guy, Ivy, Bevi(?), Sue}
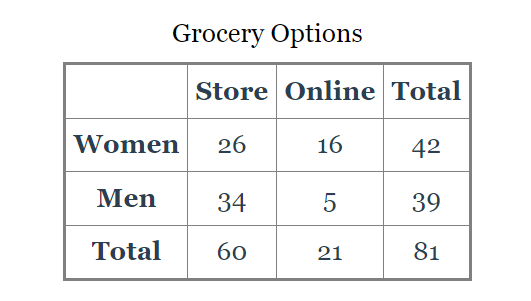
What is the probability that a person chosen at random is a man and that they shop online?
5/81
6%
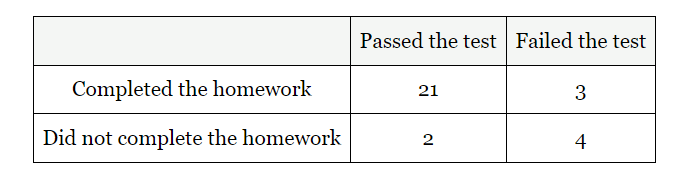
What is the probability that a student who did not completed the homework failed the test?
4/6
2/3
66%
True or False:
If two events are independent that means that probability of one event occurring has no affect on the probability of the other event occurring.
True