Determine whether the sequence is arithmetic, geometric or neither.
1/2, 1/4, 1/8, 1/16
Geometric
Select the ordered pair that is a solution to the equation represented by the graph 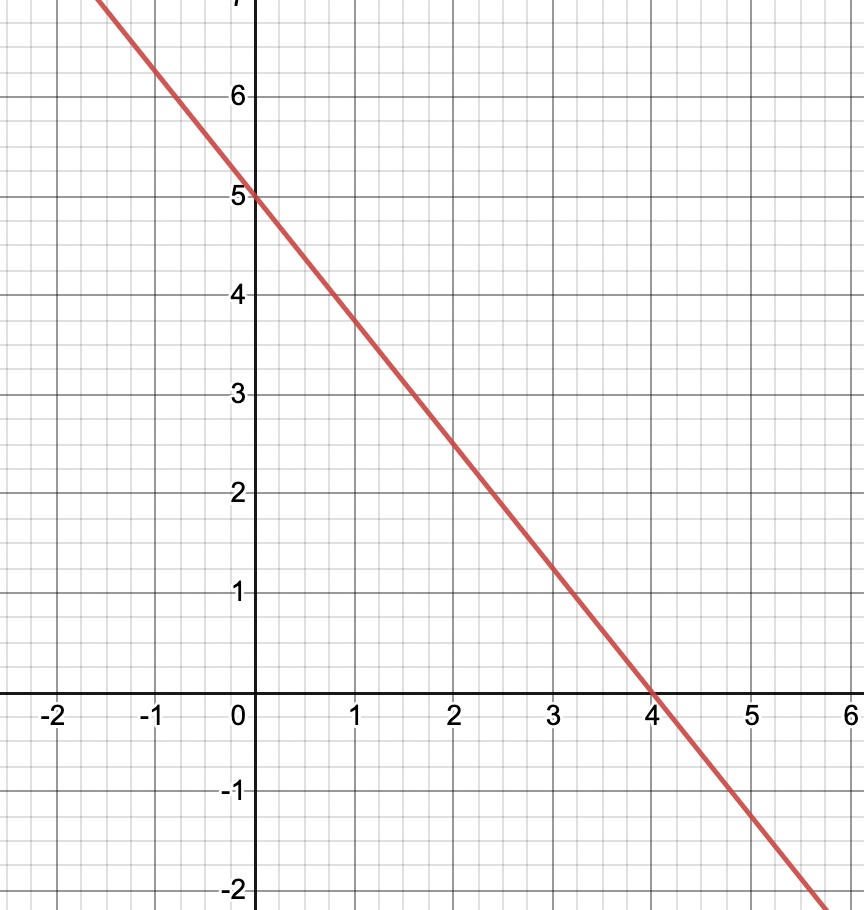
A. (4,0)
B. (2,3)
C. (5,0)
D. (3,2)
A
Given the equation of a line in point-slope form, find one point that passes through the line
y-1=4(x+3)
(1, -3)
Determine the y-intercept of the linear equation (write your answer as a coordinate (x,y))
y=3/2x+6
(0,6)
The graph shows the amount of gas, in ounces, in a lawn mower gas tank, modeled as a function of time. 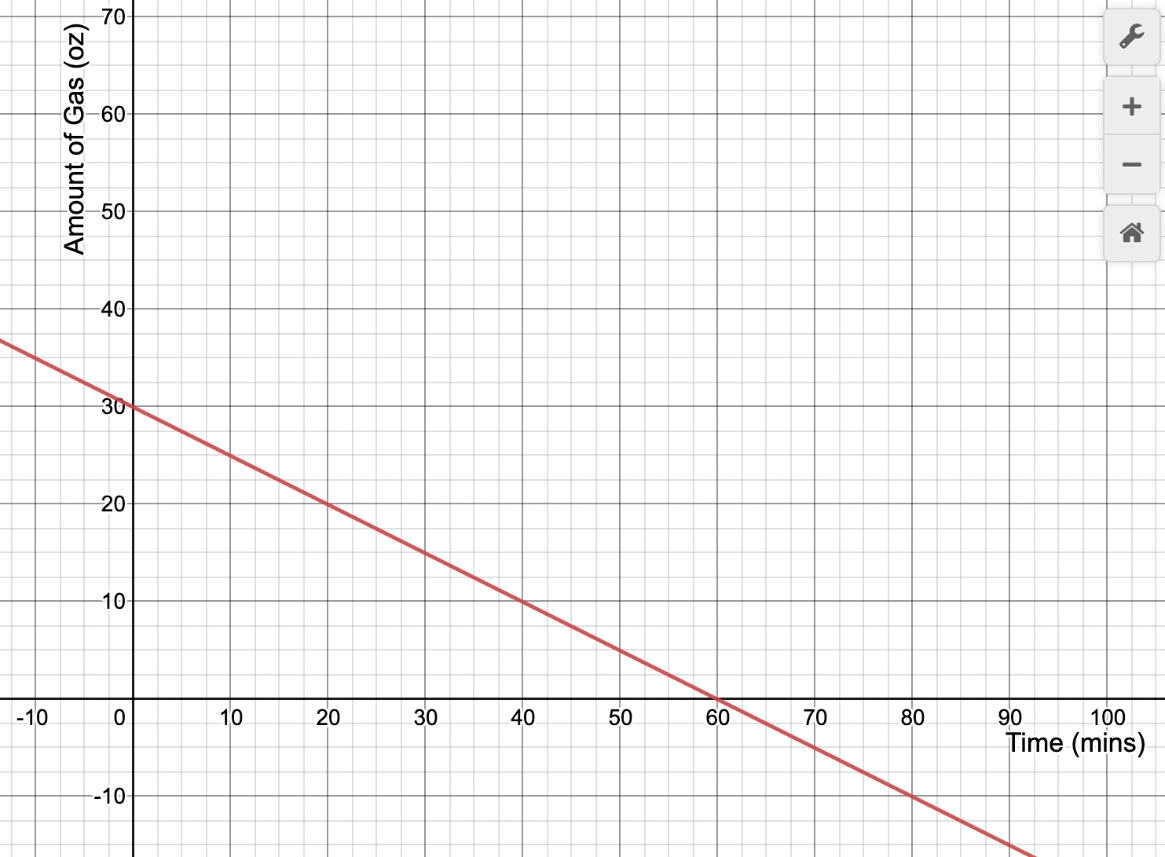
Determine whether the statement is true or false.
The maximum amount of gas in the gas tank was 60 ounces.
False
Determine the common ratio of the geometric sequence
3, -9, 27, -81
-3
Select the ordered pair that is a solution to the equation represented by the graph
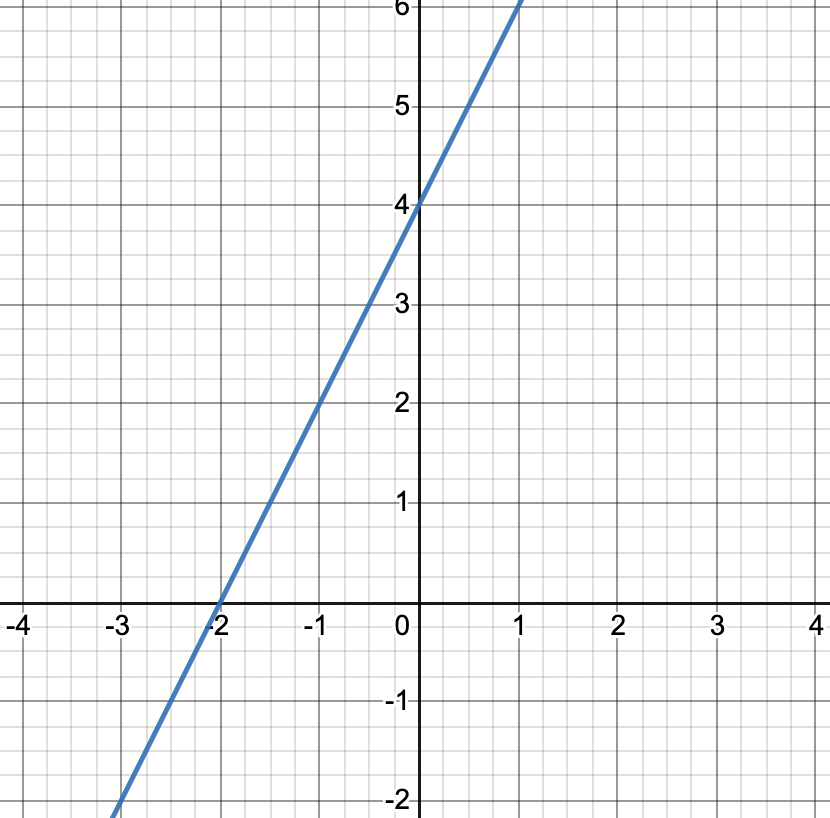
A. (-4,4)
B. (-2,0)
C. (-2,4)
D. (4,0)
B
Write a linear equation in slope-intercept form given the table 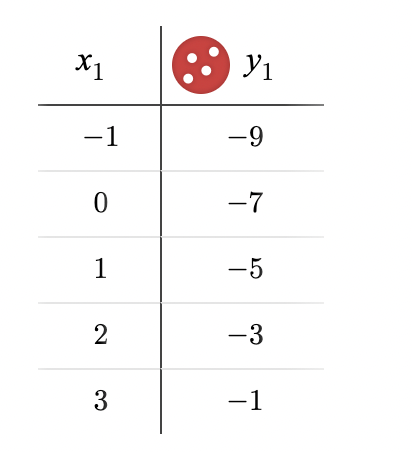
y=2x-7
Calculate the slope of the line passing through
(0, -2) and (3, 4)
2
The graph shows the amount of gas, in ounces, in a lawn mower gas tank, modeled as a function of time. 
Determine whether the statement is true or false.
The amount of gas in the gas tank is at a maximum at 0 minutes.
True
Write a recursive formula for the sequence
9, 14, 19, 24
f(1)=9
f(n)=f(n-1)+5 for n>=2
Write a linear equation in slope-intercept form for the graph
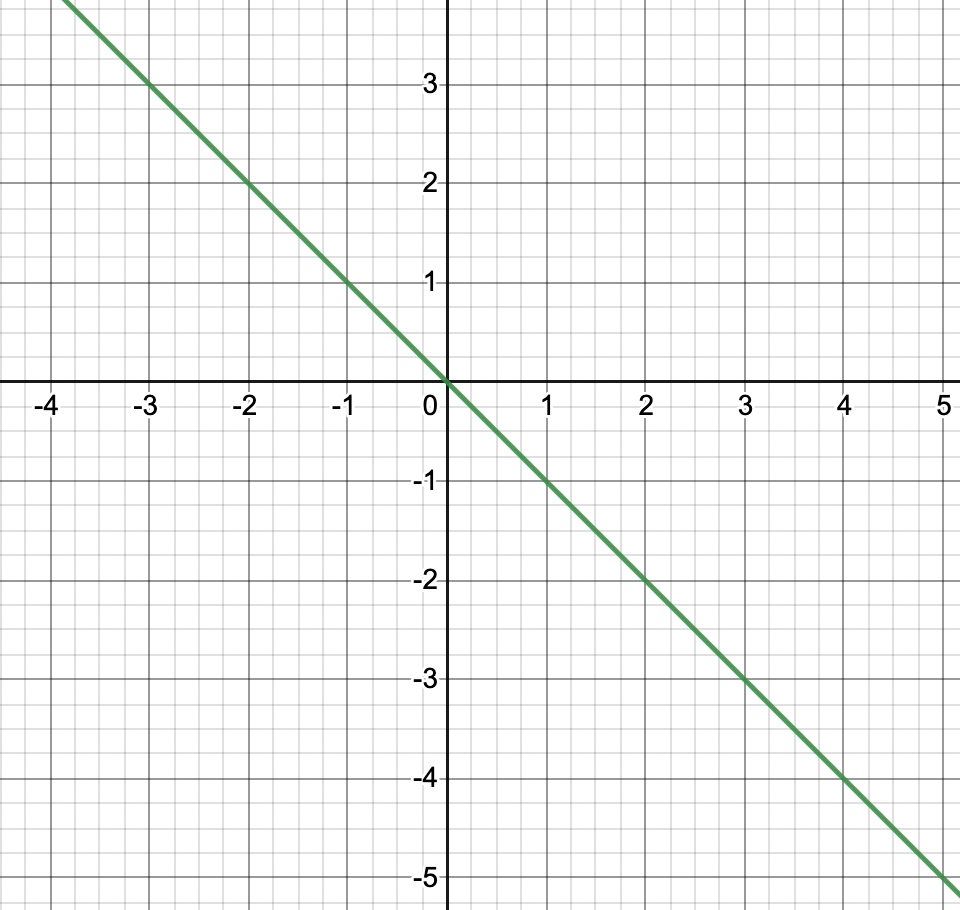
y=-x
Write the equation of the line in slope-intercept form that passes through (0, 2) and (3,1)
y=-1/3x+2
Find the x and y intercepts of the equation
x+6y=12
x-intercept (12, 0)
y-intercept (0, 2)
The graph shows the amount of gas, in ounces, in a lawn mower gas tank, modeled as a function of time. 
Determine whether the statement is true or false.
The gas tank will be empty after 60 minutes.
True
Write an explicit equation for the sequence given the recursive formula
f(0)=-10
f(n)=f(n-1)+10 for n>=1
f(n)=10n-10
Graph the equation
y=-3x+2
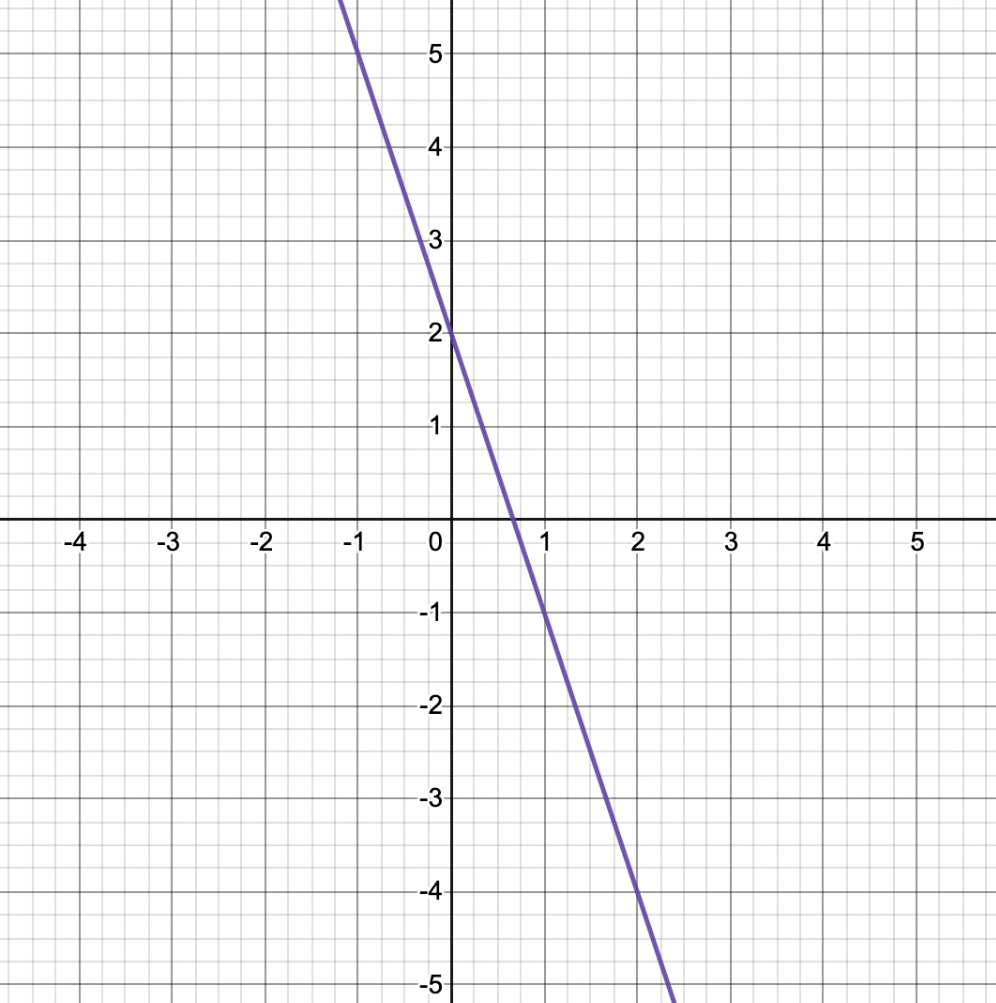
Write the equation of the line that passes through the points (2,1) and (4,7) in point-slope form
y-1=3(x-2)
y-7=3(x-4)
Find the x and y intercepts of the equation
2x-5y=20
x-intercept (10, 0)
y-intercept (0, -4)
Two types of memberships are available for a water park.
-An unlimited use membership for $70 per month or
-A monthly $10 fee plus $5 per visit
Write an equation that can be used to find the number of visits (v) per month needed for the two membership types to cost the same amount.
(Hint: Write an equation for each case and set them equal to each other)
10+5v=70