DTR
RTD
All angles for an angle.
Quadranting
It should be exact
Solving it right!
Wording the angles
Coordinating right
100
0 degrees
0 radians
100
0 radians
0 degrees
100
Graph showing the direction, label initial side and terminal side, find a coterminal angle between 0 and 2π, and find its reference angle.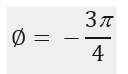
Coterminal =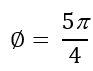 
Reference =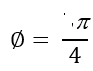 
100
What is the quadrant for the terminal side of an angle Φ if its sec > 0 and tan < 0?
Quadrant IV
100
Find the exact value of tan (-45). (Do not use calculator).
-1
100
Solve triangle with the following info:
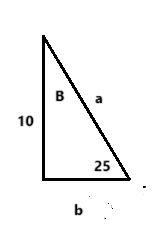
a = 23.66
B = 65 degrees
b = 21.44
100
A kite flying in the air has a rope that measures 12 ft. It projects a shadow on the ground that measures 8ft. What is the height of the kite?
8.9 ft
100
Suppose that (5/13, y) is a point in quadrant IV that is found in the unit circle. Find y. Write an exact value, not a decimal approximation.
y = -12/13
200
210 degrees
7/6 pi radians
200
pi/3
radians
60 degrees
200
Graph showing the direction, label initial side and terminal side, find a coterminal angle between 0 and 2π, and find its reference angle.
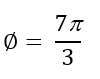
Coterminal angle:
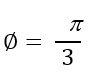
Reference angle
200
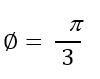
What is the quadrant in which the terminal side of angle Φ if tan < 0 and sin < 0?
IV
200
Find the exact value of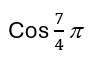 
Do not use calculator, use unit circle coordinates.
200
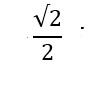
Solve for the following triangle.
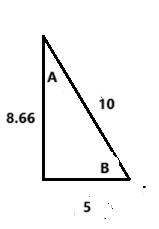
B = 60
A = 30
200
The top end of a ladder is resting on the side of a building at a height of 12ft. The bottom end of the ladder is resting at a horizontal distance of 10ft from the bottom of the building. What is the length of the ladder?
15.6 ft
200
Suppose that (x, 5/6) is a point in quadrant I that is found on the unit circle. Find x, write the exact value not a decimal approximation.
x = sqrt11 /6
300
-45 degrees
-pi/4 radians
300
2/3 pi radians
120 degrees
300
Graph showing the direction, label initial side and terminal side, find a coterminal angle between 0 and 360, and find its reference angle.
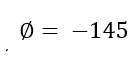
Coterminal angle:
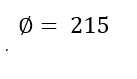
Reference angle:
300
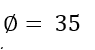
What is the quadrant in which the terminal side of Φ lies if its cos > 0 and cot > 0?
I
300
Find the exact value of sec(pi/2). DO NOT USE CALCULATOR, use unit circle coordinates.
Undefined
300
Solve the following right triangle.
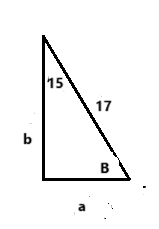
b = 16.42
a = 4.4
B = 75
300
A kite flies at a vertical height of 91 ft from the ground and its rope is very tense. The elevation angle of the kite is 57 degrees. Find the length of the rope.
108.5 ft
300
Suppose that Φ is an angle in standard position with a terminal side intersecting the unit circle in
(5/6, -sqrt11 /6)
Find exact values for cotΦ, cscΦ and cosΦ
cot Φ = -5sqrt11 /11
csc Φ = -6sqrt11 / 11
cos Φ = 5/6