Trig derivatives
Related Rates
Implicit Differentiation
Exponential and Log derivatives
Chain Rule
100
Tan(x)
Sec^2(x)
100
Differentiate with respect to t
v=(4/3)πr3
dv/dt = 4πr2(dr/dt)
100
Differentiate with no respect
y+1=x
dy=dx
100
e^x
e^x
100
(x+1)^10
10(x+1)^9
200
xsin(x)
Sin(x) + xcos(X)
200
Suppose x and y are both differentiable functions of t and are related by the equation y=x2-3x. Find dy/dt when x=3 give that dx/dt=2, when x=3.
dy/dt = 6
200
x+y=0
dx+dy=0
200
4^x
4^x*ln(4)
200
(2x)2
4(2x)
300
sec(2x)
tan(2x)sec(2x)*2
300
A pebble is dropped into a calm pond, causing ripples in the form of concentric circles. The radius r of the outer ripple is increasing at a constant rate of 1 foot per second. When the radius is 4 feet, at what rate is the total area of the disturbed water changing?
dA/dt = 8π ft2/sec
300
x2+y2=16
2dx+2dy=0
300
ln(x)
1/x
300
3(4x+7)2
24(4x+7x2)
400
csc(x)+1
-csc(x)cot(x)
400
Air is being pumped into a spherical balloon at a rate of 800 cubic centimeters per minute. How fast is the radius of the balloon changing at the instant the radius is 30 centimeters? (V=(4π/3)r3)
2/9π cm3/min
400
Solve for dy/dx
x3+y3=xy
dy/dx=(y-3x2)/(3y2-x)
400
log(x)
That is, the common log, or log based 10
1/(x*ln(10))
400
e(2x^2+4x)
(4x+4)e(2x^2+4x)
500
cot(3x+1)
-csc^2(3x+1)*3
500
The top of a 25-foot ladder is sliding down a vertical wall at a constant rate of 3 feet per minute. When the top of the ladder is 7 feet from the ground, what is the rate of change of the distance between the bottom of the ladder and the wall?
dx/dt=7/8
500
3^(x^2)
3^(x^2)ln(3)*2x
500
500
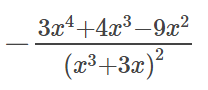
(5x2+3x-1)½
23/10