Dilations
Scale Factor
Similarity
Random
Rigid Transformations
100
Define "dilation"
When a shape increases/decreases by a given scale factor on all sides of the shape from its center of dilation.
100
When the scale factor is greater than 1, the figure gets ___________
Larger / its an enlargement
100
Are all congruent polygons also similar? Why or why not?
Yes. All congruent polygons are also similar because the same scale factor (1) is applied to all of the sides and their corresponding angles are always congruent.
100
Similar figures are ____ congruent.
(sometimes, always)
Sometimes
100
To "flip" a figure over a line
Reflection
200
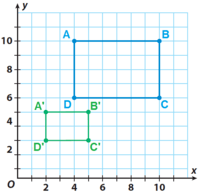Is this a Dilation? and WHY
Yes -- explanations may vary
-scale factor is 1/2 for each side, it is a reduction
200
When the scale factor (k) is 4/5, the figure gets ________________
smaller / its a reduction
200
Solve the following proportion: x / 12 = 8 / 6
x = 16
200
Similar or not similar
Not similar
200
To "slide" a figure.
Translation
300
If a triangle has side lengths 4, 8, and 10, what are the side lengths if a scale factor of 3 is applied?
12, 24, and 30.
300
When the scale factor is 1, what happens to the figure?
The figure remains the same/congruent
300
Are the following figures similar? Why or why not?
No. A different scale factor is being applied. To get from 12 to 18, the scale factor is 1.5. However, to get from 26 to 32, the scale factor is 1.23.
300
Find the scale factor. Figure EFGH is the original.
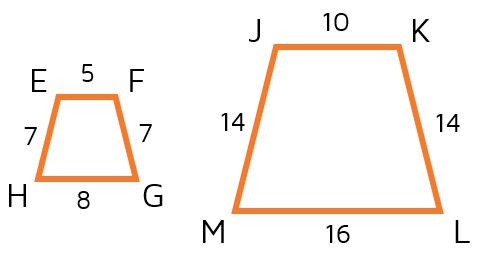
Scale Factor = 2
300
To "turn" a figure clockwise or counter clockwise
Rotation
400
If a triangle has side lengths of 16, 20, and 32, what are the side lengths if a scale factor of 1/4 is applied?
4, 5, and 8.
400
Identify the scale factor from Pre-Image A to Image B in the Graph below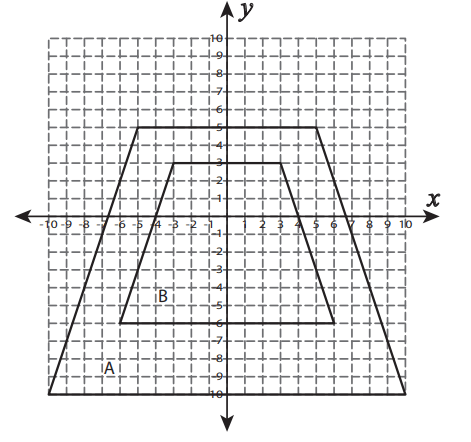
k = 3/5 (must be in most simplified form --6/10 is a correct ratio but not most simplified)
400
The following triangles are similar. Find line segment JK.
JK = 7.5
400
Dilations need these two things.
1) Center Point of Dilation
2) Scale Factor
400
When we describe a translation we need to be sure to say:
Direction and Distance
500
Dilate the following coordinates by a scale factor of 1/5 with the origin as the center of dilation:
A(10, 15) , B(-10, 0) , C(25, 30) , D (0, -20)
A' (2, 3) , B' (-2, 0) , C' (5, 6) , D' (0, -4)
500
What is the scale factor in the pictured Dilation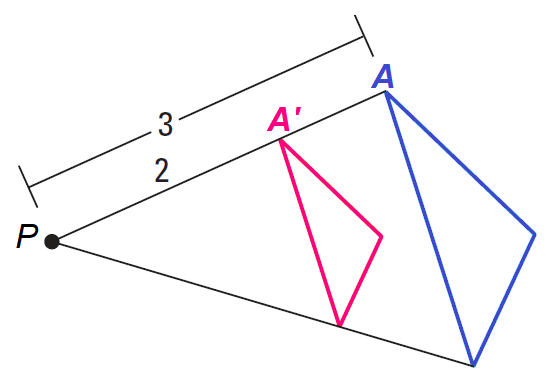
k = 2/3
500
Are the following polygons similar? Why or why not?
Yes, they are similar. Their corresponding angles are congruent and all of the side lengths share the same scale factor of 1.67.
500
These two triangles are similar. Find the missing side lengths.
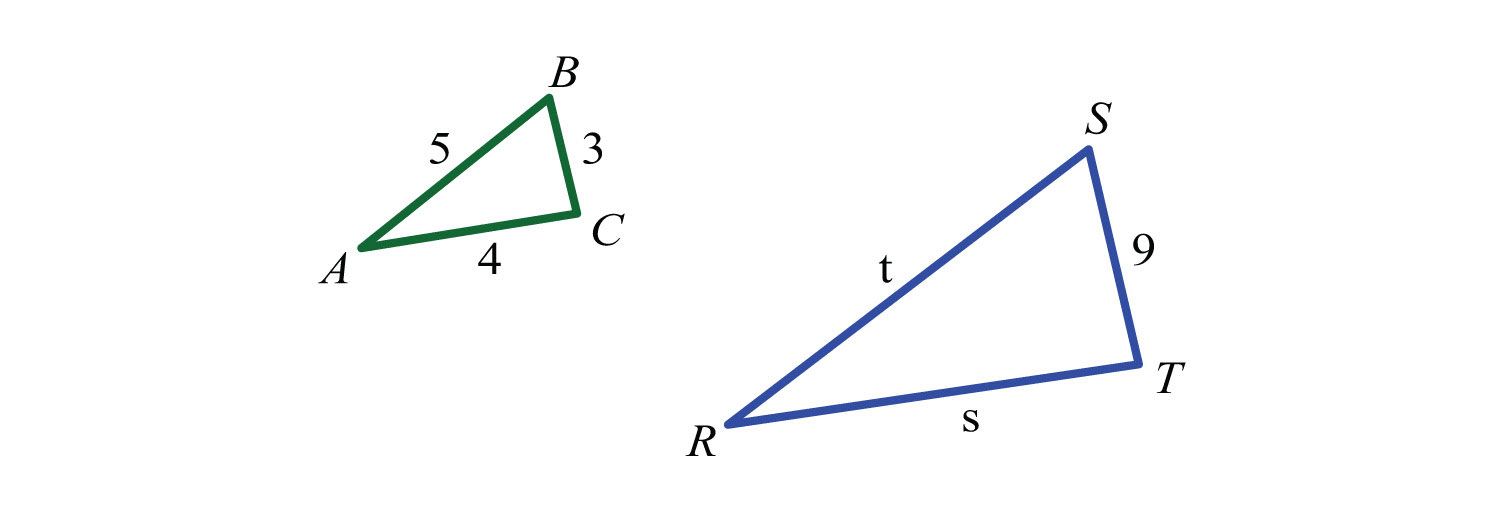
s=12
t=15
500
Describing a rotation requires these three things.
1) Center (Point)
2) Rotation angle (Degrees)
3) Direction (Clockwise or Counterclockwise)