What direction does this parabola open?
y=-x2+3x+10
Where is this function increasing? y=3x² +1
Hint: write you answer as: ___<x<___
0<x<∞
At a festival, pumpkins are launched with large catapults and air cannons. On one launch, the height of a pumpkin in feet above the ground after t seconds is modeled by h=40+120t-16t2
From what height was the pumpkin launched?
40 feet
Factor the following Quadratic Equation
x2-16=0
(x+4)(x-4)
Solve the following Quadratic Equation
x2-16=0
x=-4 and x=4
Name a real world application of quadratics.
examples: anything launched or shot into the air, dimensions when determining area of a square or rectangle, ________
What is the y-intercept of the following quadratic?
y=3x2-12x+10
(0,10)
What is the vertex of this function? y=3x² +1
(0,1)
Dane punts a football during practice? The height (h) in feet of the ball after t seconds can be modeled by the quadratic function h(t) = –16t2 + 32t. Would the maximum height of the ball be the x or the y coordinate of the vertex?
Y
Factor the following Quadratic Equation
x2+7x+10=0
(x+5)(x+2)
Solve the following Quadratic Equation
x2+7x+10=0
x=-5 and x=-2
What is the name of the point that a quadratic changes direction?
Vertex
What is the vertex of the following function?
y=(x-4)(x+2)
(1, -9)
What is the range of this function? y=3x² +1
y≥ 1
At a festival, pumpkins are launched with large catapults and air cannons. On one launch, the height of a pumpkin in meters above the ground after t seconds is modeled by h=6+5t-t2
What part of the graph would tell us how long the pumpkin was in the air?
The x-intercept
Factor the following Quadratic Equation
x2-8x+15=0
(x-3)(x-5)
Solve the following Quadratic Equation
x2-2x-15=0
x=-3 and x=5
Solve for t? d=t² + x
t=√d-x
What are the SOLUTIONS of the quadratic?
y=2x2-12x+10
x=5 and x=1
Does the function have a minimum or maximum?
How many roots?
y=3x² -1
Minimum
2 real roots
A flare is lunched up with an initial velocity of 64 feet per second from the top of a 200 foot building. The equation h(t)=-16t2+16t+96 models this situation. Determine the time it takes for the flare to reach it's maximum height.
0.5 seconds
Solve the equation using the zero product property?
(2x+3)(x-1)=0
x=-3/2 x=1
Solve the following Quadratic Equation
9x2-9x-18=0
x=-1 and x=2
What are the solutions for the parabola below? 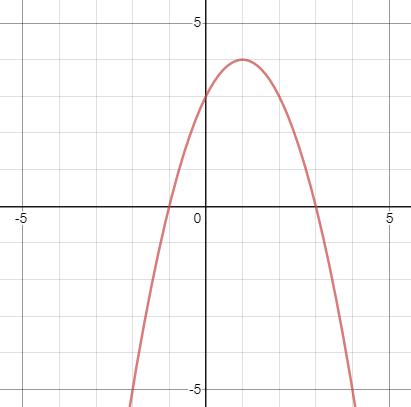
What are the x-intercepts of the following function?
y=-x2+3x+10
x=-2 and x=5
Simplify the product of (3x-4)2
9x2-24x+16
At a swim meet, Janet dives from a diving board that is 20 feet high. Her position above the water is represented by the equation y=-16x2+12x+40, where x represents the time in seconds and y represents the height above the water. After how many seconds does Janet enter the water?
2 seconds
Factor out -4
y=-4(4x2-3x-10)
y=-4(4x+5)(x-2)
x=-5/4 or x=2 (only 2 is positive)
The area of a rectangle is represented by the equation 3x2+17x+10. Find the dimensions of the rectangle in terms of x.
(x+5)(3x+2)
Solve the following Quadratic Equation
2x2+5x-3=0
x=-3 and x=1/2
Describe the translation of the graph of the function y=(x-2)² +3 to the graph of the function y=(x+4)² +1
Down 2 and Left 6