For the function below, find the vertex, axis of symmetry, and decreasing interval
y=3(x-4)^2 + 6
Vertex: (4, 6)
Axis: x = 4
Decreasing Interval:
(-infty,4)
Factor completely:
8ax+4bx-2ay-by
(4x-y)(2a+b)
State the x-intercept and y-intercept of:
y = -4^x
x intercept: none
y-intercept: (0, -1)
Write the solutions of the statement in interval notation:
x < 6 and x < 10
(-oo,6)
Find the average rate of change for [-1, 2]
y=-3x^2 + 8x - 5
5
Factor completely:
x^2(a+b) - 10(a+b)x + 16(a+b)
(a+b)(x - 8)(x - 2)
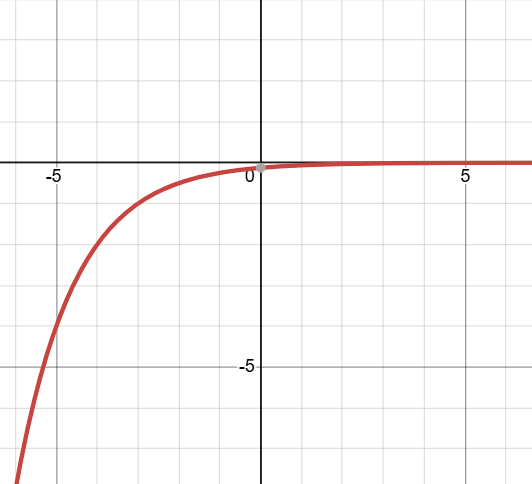
Sketch a graph of:
y = -(1/2)^(x + 3)
Find the exact value of x. 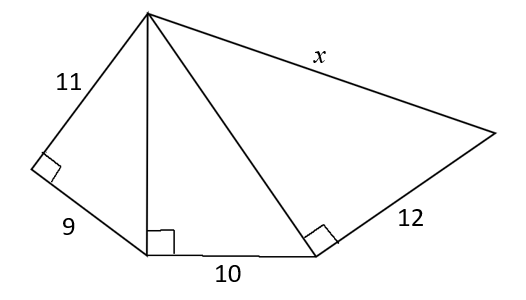
sqrt446
Where is the vertex:
y= x^2 + 10x + 33
(-5, 8)
Factor:
64x^2 - 9y^2
(8x + 3y)(8x - 3y)
State the domain and range of:
y = 3^-x
Domain: All reals
Range:
(0, infty)
Find (-x)-3 if
2(x + 5) - 8 = -7x - 16
1/8
Fill in the blanks to complete the square and discover the vertex:
y = x^2 - 18x + 83
y = x^2 - 18x + "_____" + 83 "______"
y = (x-"____")^2 +"_____"
81; -81; 9; 2
Vertex = (9, 2)
Factor completely:
12x2 - 6x - 6
6(2x + 1)(x - 1)
Find the average rate of change from x = 0 to x = 3 for the function below.
y = -5^x
-124/3
Find the GCF of
25x^2y^3 " and " 40x^7
5x^2
A launched object follows the parabolic path below where y = height in meters after x elapsed seconds. Find the maximum height and how long it takes reach that height.
y= -4.9x^2+ 29.4x
Max height = 44.1 meters, after 3 seconds.
Factor completely:
15x2 - 17x - 4
(5x + 1)(3x - 4)
Where is the function increasing?
y = (3/4)^x
(-infty,infty)
Solve:
12x^2-28x+5=0
x = -1/6 or 5/2