Linear Equations
Exponents and Polynomials
Factoring
Exponential Functions
Quadratic Functions
Solving Quadratic Functions
Systems
Random
100
Find the slope of the line that passes through the following sets of ordered pairs:
a. (6,11) and (9,26)
b. (14,-5) and (-10,7)
a. 5
b. -1/2
100
Write an expression to represent the area of the rectangle with the dimensions shown below
128a6b13
100
Factor 32x+64
32(x+2)
100
Find the equation:
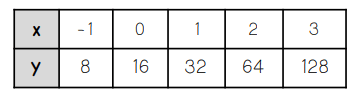
y=16(2)x
100
List the axis of symmetry, vertex, min/max, domain, and range of this function
p(x)=2x2-20x+60
AoS: 5
(5,10)
min: 10
D: All real numbers
R: y≥10
100
What is the discriminant?
What does it tell you?
b2-4ac
Tells you the number of solutions.
if the d=0----> 1 solution
If it is a d>1 then there is 2 solutions
if it is d<1 then there is no real solutions
100
Solve the systems of equations by graphing.
(2,6)
100
Factor the trinomial
2x2+6x-8
2(x-1)(x+4)
200
Find the slope of this line:
6x-5y=30
6/5
200
Simplify the expression:
8x^2+(2x-3x^2)-(9x+5)
5x2-7x-5
200
Factor x2-13x+36
(x-4)(x-9)
200
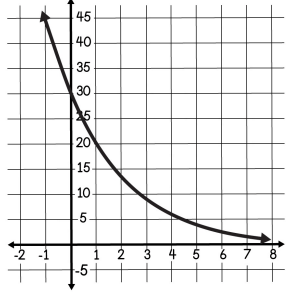Write the equation:
y=30*(2/3)^x
200
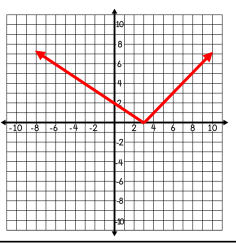
Timothy threw the football during the game Friday night. The graph shows the height of the ball and the horizontal distance of the ball in feet. Find the domain and range.
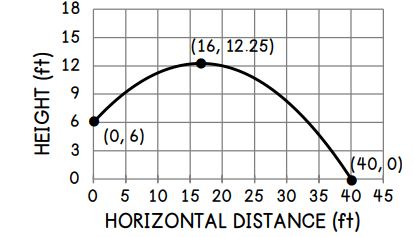
D: 0≤x≤40
R: 0≤y≤12.25
200
solve and simplify: 3(x-4)2=30
x=4+-√10
200
Solve the system of equations
x+y=15
-2x+5y=-2
(11,4)
200
Which of the functions represent exponential functions.
And are they growth or decay?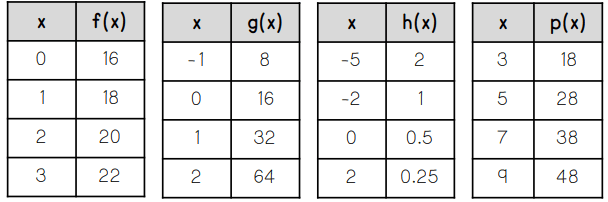
g(x) ----> Growth by a factor of 2
h does not count because the x values are not changing at a constant interval.
300
A pottery studio charges a set fee for birthday parties plus $12.958 for each person at the party. Annalise's birthday party for 8 people cost $198.60.
a. Write an equation in point slope form to represent the situation.
b. What is the y-intercept, and what does it represent?
y-198.6=12.95(x-8) b. 98; the set fee for a party is $95
300
Simplify the expression:
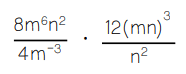
24m12n3
300
Lionel's rectangular projection screen has an area of 4x2+12x-27 units2. Write expressions to represent the dimensions of the screen.
(2x-3)(2x+9)
300
The population of two cities in 1970 are given. Write a function to represent each situation, where x represents the years after 1970.
a. Since 1970, Propers population grew at a rate of 17.5% each year
b. Since 1970, Winniford's population decreased at a rate of 8% each year.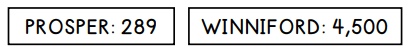 
a. y=289(1.179)x
b. y=4500(0.92)x
300
If h(x) was a result of a vertical shift down 10 and right 8, what would the function be wrote as.
h(x)=(x-8)2-10
300
Write a quadratic equation in standard form that has solutions of x=-5 and x=8
x2-3x-40=0
300
Use the discriminant to determine the number of real solutions to the system of equations below.
y=x2+12x+39
y=4x+5
Hint: b2-4ac and first step is to set equal to each other
no real solutions
300
Solve the equation:
x2-18x+81=0
x=9
400
A line passes through the points (-8,6) and (4,-3). Write an equation of the line in point-slope form.
y+3=-3/4(x-4)
y-6=-3/4(x+8)
400
Write an expression for the area of the triangle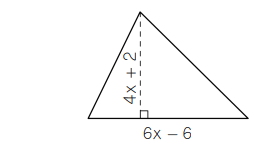
12x2-6x-6
400
Factor:
50x2-32
2(5x+4)(5x-4)
400
Oscar is studying a bacterial sample and finds the function f(x)=125(1.09)x represents the number of bacteria in the sample after x hours.
Find the number of bacteria in the sample after 12 hours. Round to the nearest tenth.
At what rate is the bacteria increasing or decreasing, and at what rate?
351.6
increasing at a rate of 9% per hour.
400
The function h has a vertex at (5,0) and passes through the point (2,27) Write an equation h(x) in vertex form.
h(x)=3(x-5)2
400
solve by completing the square:
x2+4x=15
x=-2+-√19
400
Solve the system of equations
y=x2+9x-144
y=9x
(-12,-108) and (12,108)
400
500
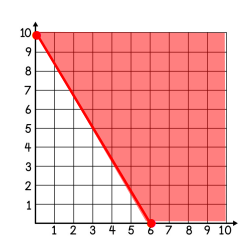
Annette works in a beauty salon. She charges $75 for hair coloring and $45 for haircuts. Annette would like to earn at least $450. Let x represent the number of hair colorings and y represent the number of haircuts. Write and inequality to represent the possible combinations.
Bonus (candy) if you can sketch a correct graph.
45x+45y>_ 450 (or equal to)
500
(6x^2-11x-10)/(2x-5)
Find the quotient
3x+2
500
Factor:
9x2-12x+4
(3x-2)2
500
Find the domain and range of the portion of the exponential function shown.
-3≤x≤5
10≤y≤60
500
Preeti graphs a quadratic function g(x) which has a vertex at (-5,10) and a y-intercept at -15. Write a function in standard form to represent g(x).
g(x)=-x2-10x-15
500
Solve by using the quadratic formula. Round your solutions to the nearest hundredth.
3x2-x-5=0
x=1.47 and x=-1.14
500
y=x2-4x-4
y=-4x+5
(3,-7) and (-3,17)
500
Write a quadratic equation that represents the function
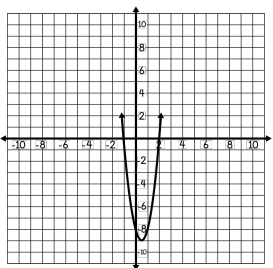
y=4x2-4x-8