Solve: 2x + 5 = 13
x=4
Identify the y-intercept of the function f(x) = 2x + 3
3
Solve the system: y = x + 2 and y = –x + 6
(2,4)
Interpret the slope in the context: A car travels at a constant speed, and the distance covered over time is represented by the equation d = 60t
2/3 + 5/7
29/21 or 1 8/21
Solve:
3(x – 4) + 2(x + 5) = 4x + 6
x=8
Describe the end behavior of the function
f(x) = –x² + 4
maximum
Solve the system: 2x + y = 7 and x – y = 1
(8/3, 5/3)
Compare the y-intercepts of f(x) = 2x + 3 and g(x) = 2x – 5
3 is positive
-5 is negative
difference of 8
The ages of five students are: 16, 17, 16, 18, and 17.
a) Find the mean age.
b) Find the mode of the ages.
mean: 16.8
mode:16 and 17
Solve:
(1/2)(x – 4) + (1/3)(x + 2) = 5
x=38/5 or 7.6
Given the graph of a function, identify its maximum point
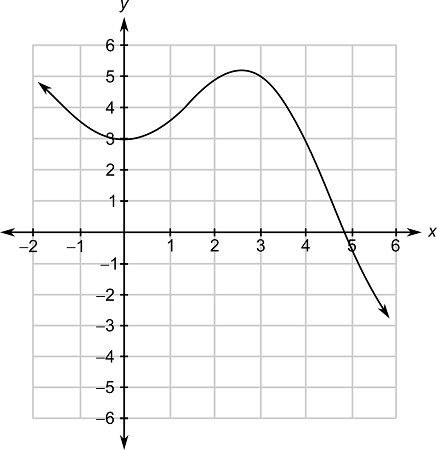
(2.5, 5.1)
Determine if the system has one solution, no solution, or infinitely many: 3x – 2y = 6 and 6x – 4y = 12
infinite solutions
Given a table of values, determine the relationship:
x: -1 0 1 2
y: 27 16.2 9.72 5.832
exponential
ratio = 0.6
Which number is the only one whose meaning can be written in the same number of letters?
four
Solve:
2(3x−4)+5=3(2x+1)−2
no solution
What is the average rate of the function f(x)=x^2+4x+5 from year 1 to year 3?
8
Solve the system: x + 2y = 5 and 3x – y = 4
(13/7 ,11/7)
A new phone app had 500 downloads in its first week. The number of downloads doubles every week after that.
a) Write an exponential function that models the number of downloads after t weeks.
b) How many downloads will the app have after 6 weeks?
c) After how many weeks will the number of downloads exceed 64,000?
D(t)=500⋅2^t
32,000 downloads
week 8
A population of bacteria doubles every 4 hours. If there are initially 500 bacteria, write an exponential function for the population after t hours, and find the population after 12 hours.
P(t)=500×2^(t/4)
4000
Solve:
4[2(x – 1) + 3] – x = 3(2x + 5) – 7
x = 4
Find the interval where the function f(x) = x³ – 3x is increasing
(−∞,−1)∪(1,∞)
Solve the system: 4x – 5y = –2 and 2x + y = 7
(33/14, 16/7)
Explain the significance of the x-intercept in a real-world context where y represents profit and x represents the number of units sold
The x-intercept is the point where the profit y is zero. This means:
At this number of units sold, the business breaks even — it neither makes a profit nor a loss.
Selling fewer than this number of units results in a loss (negative profit).
Selling more than this number results in a positive profit.
"Father of Calculus": who is he?
Scientist and mathematician Sir Isaac Newton was the first person to be given credit for creating calculus.