What is the slope of the line y=3x+1?
m=3
What is the equation for point slope form form?
y-y1 = m(x-x1)
Two lines that make four 90 degree angles are called what?
Perpendicular lines.
If a graph is going downwards (decreasing) what is its correlation?
Negative Correlation
Find the inverse of (10,10).
(10,10)
Find the slope of a line with the points (1,2) and (6,12)
Write a point slope equation for a line that goes through (-2,1) and a slope of -6.
y-1 = -6(x+2)
Two lines that never touch are called...?
Parallel Lines
Find the slope of the coordinates (12,5) and (17,80).
m=15
Find the inverse of the function f(x) = 20x-5.
f-1(x) = x+5/20 or f-1(x) = x/20 + 1/4
Find the y-intercept of the line with the points (4,7) and (2,6).
b=5
Turn the point slope equation y-10 = 2(x-8) into standard form.
y-2x = -6
Is this line parallel or perpendicular? Why?
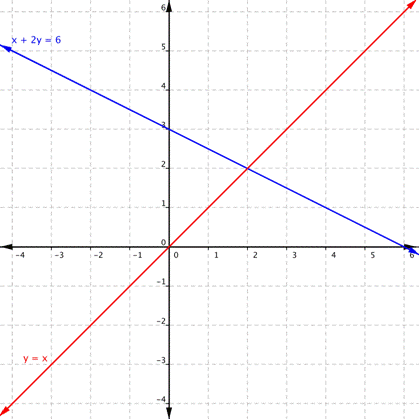
Neither. No right angles are made and the lines cross.
If the data is too random and has no connection, what correlation would the scatter plot have?
No correlation.
Find the inverses of (-30,4), (5,20), (-60,-180), and (50,-200).
(4,-30), (20,5), (-180,-60), and (-200, 50).
Write a slope-intercept equation for a line that has a slope of 3 and a y-intercept of 2.
y = 3x+2
Write the point slope equation y-11 = 3(x+4) into slope intercept form.
y = 3x + 23
Which two lines are perpendicular?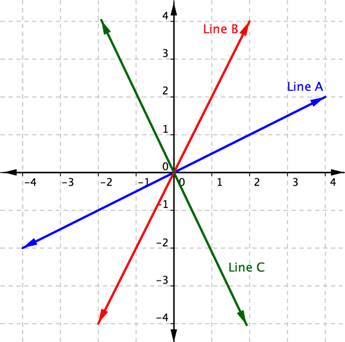
Line A and Line C
If a line starts at (0,100) and has a positive correlation, what is the y-intercept?
(0,100)
If the inverse function is f-1(x) = x+2/10, what is the original equation?
f(x) = 10x-2
What is the slope-intercept form of the graph?

y=-2x+3
Jack and Jill wanted to make a line using the points (3,-2) and with a slope of 1/4. What is the point slope form of the line?
y+2 = 1/4(x-3)
Two roads never merge and don't touch in any way. Bob says they're perpendicular and Billy says they're parallel. Who is right and why?
Billy because the two roads never meet.
Convert y-500 = 4(x-5) into slope intercept.
y = 4x+480
Why do negatives matter when you're inverting? Explain.
They don't! Inverse the function or coordinate just like you would for positives.