Function Notation
Function Fun
Function or Relation?
Functions for Life
Fearless Functions
100
Evaluate
f(x) = x + 5,
when f(10)
x = 15
100
f(x) = x^3 + 4
g(x) = 2x - 12
h(x) = x^2 - 2x + 3
Evaluate f(1)
x = 5
100
Is this a function?
Yes, because it passes the vertical line test
100
Evaluate the value of a car after 5 years.
V(t) = 20,000(0.82)^t
V(5) =
The value of the car is $7414.80 after 5 years.
100
What is the range of this graph?
[-1, 3]
200
Evaluate
f(x) = 3x - 2,
when f(5)
x = 13
200
f(x) = x^3 + 4
g(x) = 2x - 12
h(x) = x^2 - 2x + 3
Evaluate g(-2)
x = -16
200
Is this a function?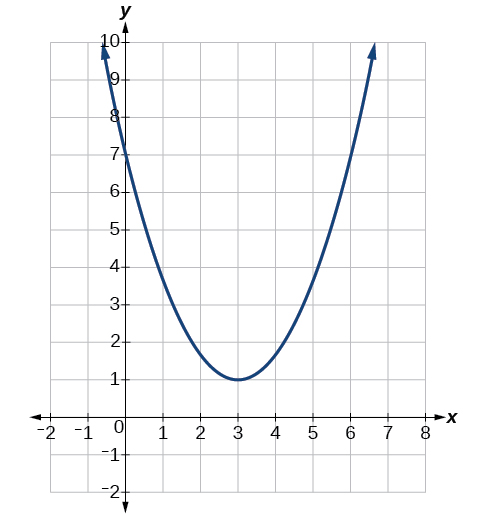
Yes it is a function, because it passes the vertical line test.
200
Evaluate the value of a car after 10 years.
V(t) = 30,000(0.82)^t
V(10) =
the value of the car is $4123.44 after 10 years.
200
What is the domain of this function?
[-5, 3]
300
Evaluate
f(x) = 2x - 6,
when f(-10)
x = -26
300
f(x) = x^3 + 4
g(x) = 2x - 12
h(x) = x^2 - 2x + 3
Evaluate f(-2)
x = -4
300
Is this a function? 
26
No, because it does not pass the vertical line test
300
Evaluate the value of a classic car after 5 years.
V(t) = 20,000(1.08)^t
V(5) =
The value of a classic car appreciates to $29,386.56 after 5 years.
300
What's the range of this graph?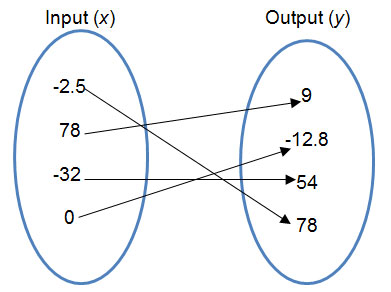
{-12.8, 9, 54, 78}
400
Evaluate
g(x) = x^2 + 5,
when g(2)
x = 9
400
f(x) = x^3 + 4
g(x) = 2x - 12
h(x) = x^2 - 2x + 3
Evaluate h(-3)
x = 18
400
Is this a function?
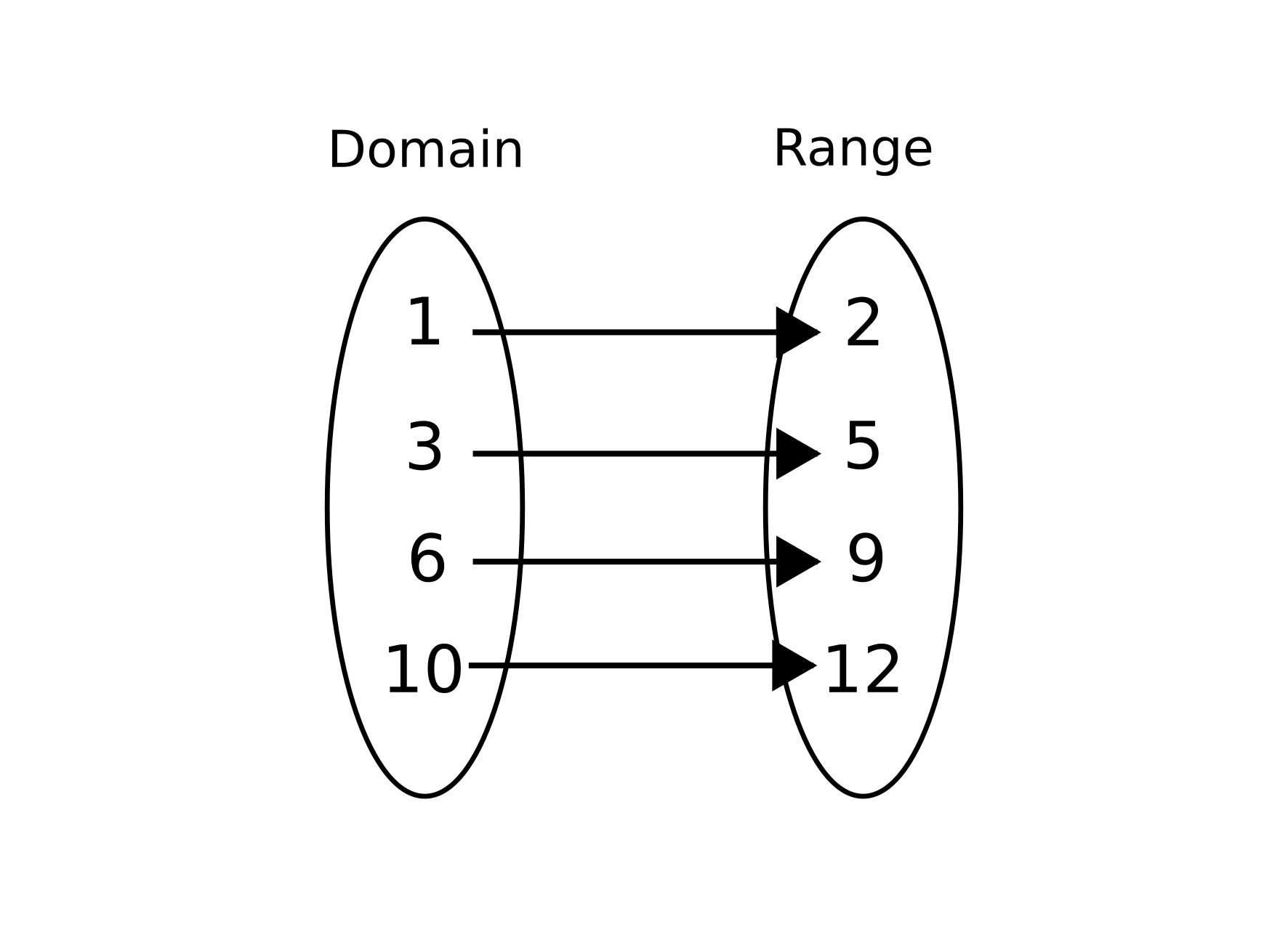
Yes, because there is one output for every input.
400
Evaluate the value of a classic car after 10 years.
V(t) = 20,000(1.08)^t
V(10) =
The value of a classic car appreciates to $43,178.50 after 5 years.
400
What is the domain of this graph?
{4, 5, 8}
500
Evaluate
g(x) = x^2 - 10,
when g(-5)
x = 15
500
f(x) = x^3 + 4
g(x) = 2x - 12
h(x) = x^2 - 2x + 3
Evaluate g(3)
x = -6
500
Is this a function?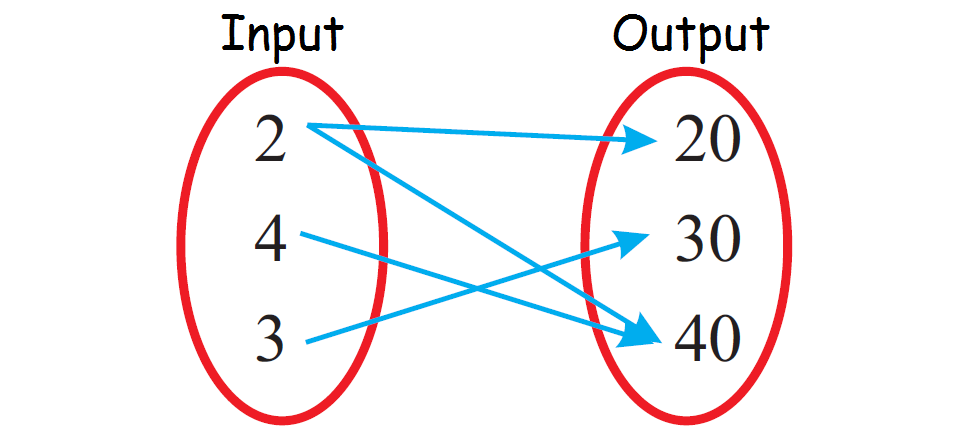
No, because 2 goes to two different outputs. So, the function is one-to-many and thus not a function.
500
How much will you have in your bank account in 30 years if you put $100 into it right now, with a 5% interest rate?
B(t) = 100(1.05)^t
You will have $432.19.
500
What's the domain AND range of this graph?
Domain: (-infiinty, infinity)
Range: [-4, infinity)